题目内容
关于x的一元二次方程(m-1)x2-2mx+m+1=0.
(1)求证:方程有两个不相等的实数根;
(2)m为何整数时,此方程的两个根都为正整数.
(1)求证:方程有两个不相等的实数根;
(2)m为何整数时,此方程的两个根都为正整数.
考点:根的判别式,一元二次方程的定义
专题:
分析:(1)表示出根的判别式,得到根的判别式大于0,进而确定出方程总有两个不相等的实数根;
(2)由(1)得到方程有两个不相等的实数根,利用求根公式表示出方程的两根:x1=
,x2=1,要使原方程的根是整数,必须使得x1=
=1+
为正整数,则m-1=1或2,进而得出符合条件的m的值.
(2)由(1)得到方程有两个不相等的实数根,利用求根公式表示出方程的两根:x1=
| m+1 |
| m-1 |
| m+1 |
| m-1 |
| 2 |
| m-1 |
解答:解:(1)∵△=b2-4ac=(-2m)2-4(m-1)(m+1)=4>0,
∴方程有两个不相等的实数根;
(2)由求根公式,得x=
,
∴x1=
=
,x2=
=1;
∵m为整数,且方程的两个根均为正整数,
∴x1=
=1+
,必为正整数,
∴m-1=1或2,
∴m=2或m=3.
∴方程有两个不相等的实数根;
(2)由求根公式,得x=
| 2m±2 |
| 2(m-1) |
∴x1=
| 2m+2 |
| 2(m-1) |
| m+1 |
| m-1 |
| 2m-2 |
| 2(m-1) |
∵m为整数,且方程的两个根均为正整数,
∴x1=
| m+1 |
| m-1 |
| 2 |
| m-1 |
∴m-1=1或2,
∴m=2或m=3.
点评:此题考查了根的判别式,以及求根公式,根的判别式的值大于0,方程有两个不相等的实数根;根的判别式的值等于0,方程有两个相等的实数根;根的判别式的值小于0,方程没有实数根.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
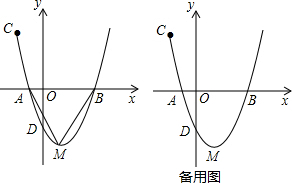 如图,已知二次函数y=x2+bx+c的图象经过两点C(-2,5)与D(0,-3),且与x轴相交于A、B两点,其顶点为M.
如图,已知二次函数y=x2+bx+c的图象经过两点C(-2,5)与D(0,-3),且与x轴相交于A、B两点,其顶点为M.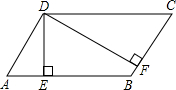 如图所示,平行四边形ABCD中,DE⊥AB,DF⊥BC,垂足分别为EF,EDF=60°,CF=3cm,AE=2cm,求?ABCD的周长.
如图所示,平行四边形ABCD中,DE⊥AB,DF⊥BC,垂足分别为EF,EDF=60°,CF=3cm,AE=2cm,求?ABCD的周长.
 已知:如图,OC=OD,OA=OB.求证:AE=BE.
已知:如图,OC=OD,OA=OB.求证:AE=BE.