题目内容
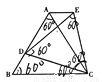
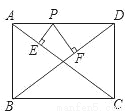
如图①,在等边三角形ABC中.D是AB边上的动点,以CD为一边,向上作等边三角形EDC.连接AE.
(l)求证:△DBC≌△EAC
(2)试说明AE∥BC的理由.
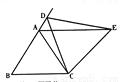
(3)如图②,当图①中动点D运动到边BA的延长线上时,所作仍为等边三角形,猜想是否仍有AE∥BC?若成立请证明.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某鞋店一天中卖出运动鞋11双,其中各种尺码的鞋的销售量如下表:
尺码(cm) | 23.5 | 24 | 24.5 | 25 | 25.5 |
销售量(双) | 1 | 2 | 2 | 5 | 1 |
则这11双鞋的尺码组成的一组数据中,众数和中位数分别是( )
A. 25,25 B. 24.5,25 C. 25,24.5 D. 24.5,24.5
A 【解析】试题分析:根据表格可得众数是25,中位数为25.

 三棱锥 B.
三棱锥 B.  长方体
长方体 正方体 D.
正方体 D.  圆柱体
圆柱体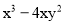 ;
; 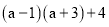
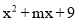 是一个完全平方式,则m=_____.
是一个完全平方式,则m=_____.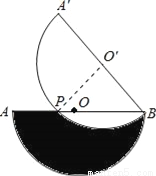

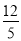 B. 2 C.
B. 2 C. 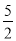 D. 1
D. 1