题目内容
 甲、乙两车分别从A、B两地同时出发,相向而行,速度不变,甲车途经C站时用1小时配货,然后按原速返回A地,乙车经C站直接到A地,乙车经C站直接到A地.如图是甲乙两车的距离y(千米)与时间t(小时)的函数部分图象,则甲车返回途中与乙车相遇时距C站的距离是
甲、乙两车分别从A、B两地同时出发,相向而行,速度不变,甲车途经C站时用1小时配货,然后按原速返回A地,乙车经C站直接到A地,乙车经C站直接到A地.如图是甲乙两车的距离y(千米)与时间t(小时)的函数部分图象,则甲车返回途中与乙车相遇时距C站的距离是考点:一次函数的应用
专题:
分析:由函数图象可以得出甲车行驶1.5小时到达C站,两车相距30千米,乙车再用0.5小时到达C站,就可以求出乙车的速度,由甲、乙两车行驶1.5小时的路程为270千米就可以求出甲、乙的路程和,进而求出甲、乙的速度和,设甲车从C站返回时需要a小时追上乙车,由追击问题的数量关系建立方程求出时间就可以得出结论.
解答:解:由函数图象可以得出:
甲、乙的速度和为:
(300-30)÷1.5=180千米/时,
乙车的速度为:30÷(2-1.5)=60千米/时,
甲车的速度为:180-60=120千米/时,
设甲车从C站返回时需要a小时追上乙车,由题意,得
60×0.5+60a=120a,
解得:a=0.5.
甲车返回途中与乙车相遇时距C站的距离是:120×0.5=60千米.
故答案为:60千米.
甲、乙的速度和为:
(300-30)÷1.5=180千米/时,
乙车的速度为:30÷(2-1.5)=60千米/时,
甲车的速度为:180-60=120千米/时,
设甲车从C站返回时需要a小时追上乙车,由题意,得
60×0.5+60a=120a,
解得:a=0.5.
甲车返回途中与乙车相遇时距C站的距离是:120×0.5=60千米.
故答案为:60千米.
点评:本题考查了相遇问题和追击问题的数量关系的运用,速度=路程÷时间的运用,列一元一次方程解实际问题的运用,解答时认真分析函数图象反应的数量关系及意义是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 由于被墨水污染,一道几何题仅能见到如图所示的图形和文字:
由于被墨水污染,一道几何题仅能见到如图所示的图形和文字:
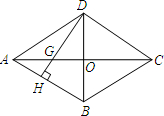 如图,四边形ABCD是菱形,对角线AC与BD交于点O,AD=BD=6cm,DH⊥AB于点H,且DH与AC交于G,则GH的长度为
如图,四边形ABCD是菱形,对角线AC与BD交于点O,AD=BD=6cm,DH⊥AB于点H,且DH与AC交于G,则GH的长度为