题目内容
19.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:| x | … | -1 | 0 | 1 | 2 | … |
| y | … | -5 | 1 | 3 | 1 | … |
| A. | 该函数图象开口向上 | |
| B. | 该函数图象与y轴交于负半轴 | |
| C. | 当x=4时,y>0 | |
| D. | 方程y=ax2+bx+c=0的正跟在2和3之间 |
分析 根据函数图象具有对称性和表格可知对称轴和顶点坐标,以及开口方向,从而可以判断选项是否正确,从而可以解答本题.
解答 解:根据表格可知,x=0和x=2时的函数值相等,二次函数图象具有对称性,
则对称轴为x=$\frac{0+2}{2}=1$.
则顶点坐标为(1,3).
∴函数图象的开口向下,与y轴的交点为(0,1).(故选项A错误)
∴函数图象与y轴交于正半轴.(故选项B错误)
∵对称轴为x=1,点(-1,-5)在函数图象上,
∴x=4和x=-2时的函数值相等,当x<1时,y随x的增大而增大.
∴x=-2时,y<0;x=4时,y<0.(故选项C错误).
∵二次函数具有对称性,点(0,1)和点(-1,-5)与点(2,2)和点(3,-5)对应,
∴方程y=ax2+bx+c=0的正根在2和3之间.(故选项D正确)
故选D.
点评 本题考查二次函数的性质,解题的关键是明确二次函数图象具有对称性,能根据图象判断出开口方向.

练习册系列答案
相关题目
8.下列说法不正确的是( )
| A. | 304.35是精确到百分位 | B. | 4.609万精确到万位 | ||
| C. | 6300是精确到个位 | D. | 近似数5.30和5.3的精确度不一样 |
9.把方程2(x-1)-3(1-x)=x,化成“ax=b”的形式为( )
| A. | 4x=5 | B. | -2x=5 | C. | 6x=5 | D. | 6x=1 |
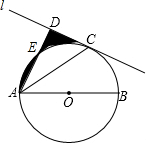 如图,AB为⊙O直径,AC为弦,过C点的直线为l,AD⊥l于点D,且AC平分∠DAB
如图,AB为⊙O直径,AC为弦,过C点的直线为l,AD⊥l于点D,且AC平分∠DAB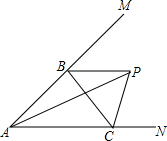 如图,点P在∠MAN内,点B,C分别是AM,AN上的点,∠MBC和∠NCB的平分线相交于点P.若∠APB=24°,则∠ACB的度数为48°.
如图,点P在∠MAN内,点B,C分别是AM,AN上的点,∠MBC和∠NCB的平分线相交于点P.若∠APB=24°,则∠ACB的度数为48°.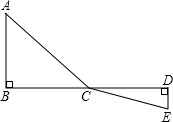 如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC,已知AB=3,DE=2,BD=12,设CD=x.
如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC,已知AB=3,DE=2,BD=12,设CD=x.