题目内容
若点(x,y)是两条直线y=x+3,y=-x+1与x轴围成的三角形内的整数点(含边界).求x、y满足y≤
的概率 .
| 1-x |
考点:列表法与树状图法
专题:计算题
分析:根据题意画出图形,找出满足题意点的坐标,找出满足y≤
的情况数,即可求出所求的概率.
| 1-x |
解答: 解:对于直线y=x+3,令x=0,得到y=3;令y=0,得到x=-3,
解:对于直线y=x+3,令x=0,得到y=3;令y=0,得到x=-3,
对于直线y=-x+1,令x=0,得到y=1;令y=0,得到x=1,
如图所示,满足题意的整数点坐标为(-3,0),(-2,0),(-1,0),(0,0),(1,0),(-2,1),(-1,1),(0,1),(-1,2)共9种,其中满足y≤
的有:(-3,0),(-2,0),(-1,0),(0,0),(1,0),(-2,1),(-1,1),(0,1)共8种,
则P=
.
故答案为:
.
 解:对于直线y=x+3,令x=0,得到y=3;令y=0,得到x=-3,
解:对于直线y=x+3,令x=0,得到y=3;令y=0,得到x=-3,对于直线y=-x+1,令x=0,得到y=1;令y=0,得到x=1,
如图所示,满足题意的整数点坐标为(-3,0),(-2,0),(-1,0),(0,0),(1,0),(-2,1),(-1,1),(0,1),(-1,2)共9种,其中满足y≤
| 1-x |
则P=
| 8 |
| 9 |
故答案为:
| 8 |
| 9 |
点评:此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
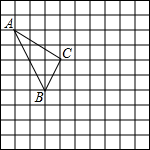 在如图的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,4),(-1,2).
在如图的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,4),(-1,2).
 如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,船P在船B的北偏西30°方向上,BP的距离为30海里.
如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,船P在船B的北偏西30°方向上,BP的距离为30海里.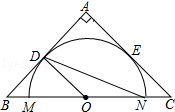 如图,在等腰直角三角形ABC中,AB=AC=4,点O为BC的中点,以O为圆心作⊙O交BC于点M、N,⊙O与AB、AC相切,切点分别为D、E,则∠MND的度数为
如图,在等腰直角三角形ABC中,AB=AC=4,点O为BC的中点,以O为圆心作⊙O交BC于点M、N,⊙O与AB、AC相切,切点分别为D、E,则∠MND的度数为 如图,在△ABC中,AB=AC=7,BC=2,点Q是BC的延长线上一点,且AQ=BQ+CQ,求tanQ=
如图,在△ABC中,AB=AC=7,BC=2,点Q是BC的延长线上一点,且AQ=BQ+CQ,求tanQ=