题目内容
4.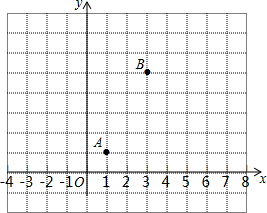 如图,在坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使|PB-PA|最大,则点P的坐标为( )
如图,在坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使|PB-PA|最大,则点P的坐标为( )| A. | (0,1) | B. | (0,2) | C. | $(\frac{4}{3},0)$ | D. | (0,-1) |
分析 连接BA并延长交y轴于P,则点P即为所求,求出直线AB的解析式y=2x-1,当x=0时,y=-1,于是得到结论.
解答 解: 连接BA并延长交y轴于P,则点P即为所求,
连接BA并延长交y轴于P,则点P即为所求,
设:直线AB的解析式为:y=kx+b,
∵A(1,1)、B(3,5),
∴$\left\{\begin{array}{l}{1=k+b}\\{5=3k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=-1}\end{array}\right.$,
∴直线AB的解析式为:y=2x-1,
当x=0时,y=-1,
∴P(0,-1).
故选:D.
点评 此题考查了一次函数综合题,涉及的知识有:三角形三边关系,待定系数法确定一次函数解析式,一次函数与坐标轴的交点,找出|PB-PA|最大值时P的位置是解本题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 如图,A(-1,0),B(5,0),C(0,5),抛物线y=ax2+bx+c过A、B、C三点.
如图,A(-1,0),B(5,0),C(0,5),抛物线y=ax2+bx+c过A、B、C三点. 如图所示,要使图中平面展开图按虚线折叠成正方体后相对面上两个数之和相等,则b-c=-7.
如图所示,要使图中平面展开图按虚线折叠成正方体后相对面上两个数之和相等,则b-c=-7.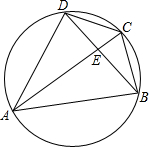 设ABCD为圆内接四边形,对角线AC平分BD于E.
设ABCD为圆内接四边形,对角线AC平分BD于E.