题目内容
14.下列语句:①在同一平面内,三条直线只有两个交点,则其中两条直线互相平行;
②在同一平面内,过一点有且只有一条直线与已知直线平行;
③平移过程中,各组对应点连成两条线段平行且相等;
④两条直线与第三条直线相交,如果内错角相等,则同旁内角互补.
⑤两平行线被第三条直线所截得的同旁内角的平分线互相垂直
⑥如果甲看乙的方向是北偏东60°,那么乙看甲的方向是南偏西30°
⑦垂直于同一条直线的两条直线平行
其中错误的有4个.
分析 根据平行公理、平移的性质和平行线的判定与性质进行判断即可.
解答 解:①在同一平面内,三条直线只有两个交点,则其中两条直线互相平行,正确;
②过直线外一点有且只有一条直线与已知直线平行,错误;
③平移过程中,各组对应点连成两条线段平行或者在同一直线上且相等,错误;
④两条直线与第三条直线相交,如果内错角相等,那么这两条直线平行,所以同旁内角互补,正确;
⑤两平行线被第三条直线所截得的同旁内角的平分线互相垂直,正确;
⑥如果甲看乙的方向是北偏东60°,那么乙看甲的方向是南偏西30°,错误;
⑦垂直于同一条直线的两条直线平行,必须是同一平面,故错误.
故答案为:4.
点评 本题考查了平行公理、平移的性质和平行线的判定与性质,熟练掌握性质与定理是解决此类问题的关键.注意平行公理是:过直线外一点有且只有一条直线与已知直线平行.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
3.二次函数y=ax2+bx+c(a,b,c为常数,a≠0)中,x与y的部分对应值如下表:
有下列结论:
①函数有最大值,且最大值为1;
②若x0满足y=ax02+bx+c,则2<x0<3或-1<x0<0;
③若方程ax2+bx+c+m=0有两个不等的实数根且m<-1;
④对于任意实数m,当m≠1时,有m(am+b)<$\frac{1}{2}$.
其中正确结论的个数是( )
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | -3.5 | -1 | 0.5 | 1 | 0.5 | -1 | -3.5 | … |
①函数有最大值,且最大值为1;
②若x0满足y=ax02+bx+c,则2<x0<3或-1<x0<0;
③若方程ax2+bx+c+m=0有两个不等的实数根且m<-1;
④对于任意实数m,当m≠1时,有m(am+b)<$\frac{1}{2}$.
其中正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4.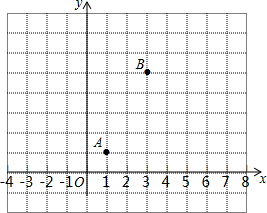 如图,在坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使|PB-PA|最大,则点P的坐标为( )
如图,在坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使|PB-PA|最大,则点P的坐标为( )
 如图,在坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使|PB-PA|最大,则点P的坐标为( )
如图,在坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使|PB-PA|最大,则点P的坐标为( )| A. | (0,1) | B. | (0,2) | C. | $(\frac{4}{3},0)$ | D. | (0,-1) |
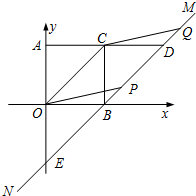 如图,在平面直角坐标系xOy内,?AOBC的顶点A、O、B、C的坐标分别为(0,1)、(0,0)、(1,0)、(1、1),过点B的直线MN与OC平行,AC的延长线交MN于点D,点P是直线MN上的一个动点,CQ∥OP交MN于点Q.
如图,在平面直角坐标系xOy内,?AOBC的顶点A、O、B、C的坐标分别为(0,1)、(0,0)、(1,0)、(1、1),过点B的直线MN与OC平行,AC的延长线交MN于点D,点P是直线MN上的一个动点,CQ∥OP交MN于点Q. 如图,菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高DH=4.8.
如图,菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高DH=4.8. 在中超联赛期间,一队员在距离球门12米处挑射,正好射中了2.4米高的横梁,已知球的最高点距球门的水平距离为3米,若足球运行的路线是抛物线,如图,求其函数解析式.
在中超联赛期间,一队员在距离球门12米处挑射,正好射中了2.4米高的横梁,已知球的最高点距球门的水平距离为3米,若足球运行的路线是抛物线,如图,求其函数解析式. 如图所示.∠AOB=90°,ON是∠AOC的平分线,OM是∠BOC的平分线,求∠MON的大小.
如图所示.∠AOB=90°,ON是∠AOC的平分线,OM是∠BOC的平分线,求∠MON的大小.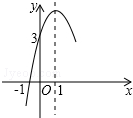 已知抛物线y=ax2+bx+c的部分图象如图所示,则不等式ax2+bx+c>0的解集为-1<x<3.
已知抛物线y=ax2+bx+c的部分图象如图所示,则不等式ax2+bx+c>0的解集为-1<x<3.