题目内容
13.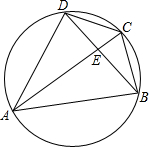 设ABCD为圆内接四边形,对角线AC平分BD于E.
设ABCD为圆内接四边形,对角线AC平分BD于E.求证:AB2+BC2+CD2+DA2=2AC2.
分析 由结论联想到运用余弦定理,则有AC2=AD2+DC2-2AD•DC•cos∠ADC,AC2=AB2+BC2-2AB•BC•cos∠ABC,只需证到AD•DC•cos∠ADC=-AB•BC•cos∠ABC.根据圆内接四边形的对角互补可得∠ADC+∠ABC=180°,从而可得cos∠ADC=-cos∠ABC,sin∠ADC=sin∠ABC,只需证到AD•DC=AB•BC,只需证到S△ADC=S△BAC,过点D作DG⊥AC于G,过点B作BH⊥AC于H,只需证到DG=BH,只需证到△DGE≌△BHE即可.
解答 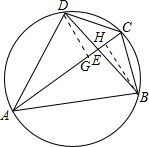 证明:过点D作DG⊥AC于G,过点B作BH⊥AC于H,如图,
证明:过点D作DG⊥AC于G,过点B作BH⊥AC于H,如图,
则有∠DGE=∠BHE=90°.
在△DGE和△BHE中,
$\left\{\begin{array}{l}{∠DGE=∠BHE}\\{∠DEG=∠BEH}\\{DE=BE}\end{array}\right.$,
∴△DGE≌△BHE,
∴DG=BH,
∴S△ADC=S△BAC,
∴$\frac{1}{2}$AD•DC•sin∠ADC=$\frac{1}{2}$AB•BC•sin∠ABC,
∵∠ADC+∠ABC=180°,
∴cos∠ADC=-cos∠ABC,sin∠ADC=sin∠ABC,
∴AD•DC=AB•BC.
在△ADC中,根据余弦定理可得,
AC2=AD2+DC2-2AD•DC•cos∠ADC.
在△ABC中,根据余弦定理可得,
AC2=AB2+BC2-2AB•BC•cos∠ABC.
∴2AC2=AD2+DC2-2AD•DC•cos∠ADC+AB2+BC2-2AB•BC•cos∠ABC
=AD2+DC2+2AB•BC•cos∠ABC+AB2+BC2-2AB•BC•cos∠ABC
=AD2+DC2+AB2+BC2.
点评 本题主要考查了全等三角形的判定与性质、三角形的面积公式、互补两角的同名三角函数的关系、余弦定理等知识,由结论的特点联想到余弦定理是解决本题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案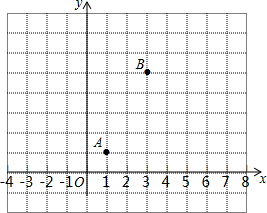 如图,在坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使|PB-PA|最大,则点P的坐标为( )
如图,在坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使|PB-PA|最大,则点P的坐标为( )| A. | (0,1) | B. | (0,2) | C. | $(\frac{4}{3},0)$ | D. | (0,-1) |
| A. | 在5与6之间 | B. | 在6与7之间 | C. | 在7与8之间 | D. | 在8与9之间 |
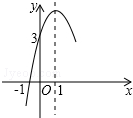 已知抛物线y=ax2+bx+c的部分图象如图所示,则不等式ax2+bx+c>0的解集为-1<x<3.
已知抛物线y=ax2+bx+c的部分图象如图所示,则不等式ax2+bx+c>0的解集为-1<x<3.