题目内容
20．
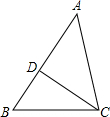如图，△ABC∽△ACD．（1）若$\frac{AB}{AC}$=$\frac{5}{2}$，AD=4cm，DC=6cm，求AC和BC的长；
（2）若∠A=58°，∠ADC=88°，求∠B的度数．
分析 （1）根据相似三角形对应边的比相等即可得到结论；
（2）根据相似三角形对应角相等即可得到结论．
解答 解：（1）∵△ABC∽△ACD，
∴$\frac{AB}{AC}=\frac{AC}{AD}$=$\frac{CD}{BC}$=$\frac{5}{2}$，
∵AD=4cm，DC=6cm，
∴AC=10cm，BC=$\frac{12}{5}$cm；
（2）∵△ABC∽△ACD，
∴∠ACB=∠ADC=88°，
∵∠A=58°，
∴∠B=180°-∠A-∠ACB=34°．
点评 本题考查的是相似三角形的性质，熟知相似三角形对应边的比等于相似比是解答此题的关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
如图所示，已知直线AB∥CD，∠C=105°，∠A=25°，求∠E的度数．
8．若五边形ABCDE中，∠A=∠B=∠C，且∠D的外角为78°，∠D的外角与∠E互余，则∠B的度数是（ ）
| A． | 142° | B． | 140° | C． | 130° | D． | 150° |
如图，∠1=∠2，AD与BE相交于点G，EF∥AD，交BC于点F．试证明：∠BEF=∠ABC．
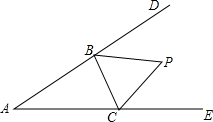如图，在△ABC中，分别延长△ABC的边AB，AC到D，E，∠CBD与∠BCE的平分线相交于点P，爱动脑筋的小明在写作业时发现如下规律：
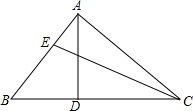如图：在△ABC中，AD⊥BC于D，点E在BA上，∠ECB=30°，若EC=2$\sqrt{3}$且BE：AE=3：2，则AD=$\frac{5\sqrt{3}}{3}$．
10．如果抛物线经过点A（2，0）和B（-1，0），且与y轴交于点C，若OC=2．则这条抛物线的解析式是（ ）
| A． | y=x2-x-2 | B． | y=-x2-x-2或y=x2+x+2 | ||
| C． | y=-x2+x+2 | D． | y=x2-x-2或y=-x2+x+2 |