题目内容
11. 如图所示,已知直线AB∥CD,∠C=105°,∠A=25°,求∠E的度数.
如图所示,已知直线AB∥CD,∠C=105°,∠A=25°,求∠E的度数.
分析 先根据平行线的性质得∠BFE=∠C=105°,然后根据三角形外角性质求∠E的度数.
解答 解:∵AB∥CD,
∴∠BFE=∠C=105°,
∵∠BFE=∠A+∠E,
∴∠E=105°-25°=80°.
点评 本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了三角形外角性质.

练习册系列答案
相关题目
20.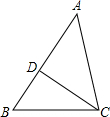 如图,△ABC∽△ACD.
如图,△ABC∽△ACD.
(1)若$\frac{AB}{AC}$=$\frac{5}{2}$,AD=4cm,DC=6cm,求AC和BC的长;
(2)若∠A=58°,∠ADC=88°,求∠B的度数.
 如图,△ABC∽△ACD.
如图,△ABC∽△ACD.(1)若$\frac{AB}{AC}$=$\frac{5}{2}$,AD=4cm,DC=6cm,求AC和BC的长;
(2)若∠A=58°,∠ADC=88°,求∠B的度数.
1. 如图所示,点O在直线AB上,图中小于平角的角共有( )
如图所示,点O在直线AB上,图中小于平角的角共有( )
 如图所示,点O在直线AB上,图中小于平角的角共有( )
如图所示,点O在直线AB上,图中小于平角的角共有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
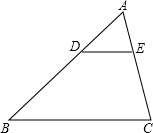 如图,已知△ABC∽△ADE,$\frac{AB}{BD}$=$\frac{5}{3}$,BC=20cm,∠BAC=40°,∠ABC=65°,求
如图,已知△ABC∽△ADE,$\frac{AB}{BD}$=$\frac{5}{3}$,BC=20cm,∠BAC=40°,∠ABC=65°,求 二次函数y=a(x+h)2的图象如图所示,已知a=$\frac{1}{2}$,OA=OC,试求该抛物线的解析式.
二次函数y=a(x+h)2的图象如图所示,已知a=$\frac{1}{2}$,OA=OC,试求该抛物线的解析式.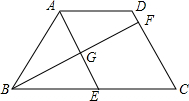 如图,在四边形ABCD中,∠BAD=∠ADC,∠ABC=∠BCD,∠BAD的角平分线AE与∠ABC的角平分线BF交于点G,
如图,在四边形ABCD中,∠BAD=∠ADC,∠ABC=∠BCD,∠BAD的角平分线AE与∠ABC的角平分线BF交于点G,