题目内容
10.如果抛物线经过点A(2,0)和B(-1,0),且与y轴交于点C,若OC=2.则这条抛物线的解析式是( )| A. | y=x2-x-2 | B. | y=-x2-x-2或y=x2+x+2 | ||
| C. | y=-x2+x+2 | D. | y=x2-x-2或y=-x2+x+2 |
分析 由于已知抛物线与x轴的交点坐标,则可交点式y=a(x-2)(x+1),再由OC=2得到C点坐标为(0,2)或(0,-2),然后把(0,2)和(0,-2)分别代入y=a(x-2)(x+1)可求出对应的a的值,从而可得抛物线解析式.
解答 解:设抛物线解析式为y=a(x-2)(x+1),
∵OC=2,
∴C点坐标为(0,2)或(0,-2),
把C(0,2)代入y=a(x-2)(x+1)得a•(-2)•1=2,解得a=-1,此时抛物线解析式为y=-(x-2)(x+1),即y=-x2+x+2;
把C(0,-2)代入y=a(x-2)(x+1)得a•(-2)•1=-2,解得a=1,此时抛物线解析式为y=(x-2)(x+1),即y=x2-x-2.
即抛物线解析式为y=-x2+x+2或y=x2-x-2.
故选D.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
20.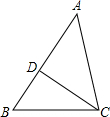 如图,△ABC∽△ACD.
如图,△ABC∽△ACD.
(1)若$\frac{AB}{AC}$=$\frac{5}{2}$,AD=4cm,DC=6cm,求AC和BC的长;
(2)若∠A=58°,∠ADC=88°,求∠B的度数.
 如图,△ABC∽△ACD.
如图,△ABC∽△ACD.(1)若$\frac{AB}{AC}$=$\frac{5}{2}$,AD=4cm,DC=6cm,求AC和BC的长;
(2)若∠A=58°,∠ADC=88°,求∠B的度数.
1. 如图所示,点O在直线AB上,图中小于平角的角共有( )
如图所示,点O在直线AB上,图中小于平角的角共有( )
 如图所示,点O在直线AB上,图中小于平角的角共有( )
如图所示,点O在直线AB上,图中小于平角的角共有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
5.已知反比例函数的图象经过点M(-1,-4),则这个函数的图象位于( )
| A. | 第一、三象限 | B. | 第二、三象限 | C. | 第二、四象限 | D. | 第三、四象限 |
 如图,∠MDF=∠EBN,∠A=∠C.
如图,∠MDF=∠EBN,∠A=∠C.


