题目内容
19.在平面直角坐标系中,点A( 1,2)关于y轴的对称点为B,点A关于原点的对称点为C,设AB与y轴的交点为D,则$\frac{{S}_{△ADO}}{{S}_{△ABC}}$=$\frac{1}{4}$.分析 利用已知得出各对应点位置,进而得出AB=2,AD=1,BC=4,DO=2,进而得出△ADO,△ABC的面积进而得出答案.
解答  解:如图所示:可得出B点坐标为:(-1,2),C(-1,-2),
解:如图所示:可得出B点坐标为:(-1,2),C(-1,-2),
则S△ADO=$\frac{1}{2}$×1×2=1,
S△ABC=$\frac{1}{2}$×2×4=4,
故$\frac{{S}_{△ADO}}{{S}_{△ABC}}$=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 此题主要考查了关于y轴对称点的性质以及关于原点对称点的性质,正确得出各对应点位置是解题关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
9.某一次函数的图象经过点(-3,6),且函数值y随自变量x的增大而增大,则下列函数中符合上述条件的是( )
| A. | y=-3x-3 | B. | y=4x+6 | C. | y=-2x+12 | D. | y=x+9 |
7.一次函数y=kx-k(k≠0),若y随x的增大而减小,则该函数的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,有一个面积为20的矩形,它的两邻边分别为x、y(2≤x≤10),则y与x的函数图象大致是( )
如图,有一个面积为20的矩形,它的两邻边分别为x、y(2≤x≤10),则y与x的函数图象大致是( )



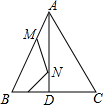 等边△ABC的边长是8,AD⊥BC,E是BD的中点,M、N分别是AB、AD上的动点,求MN+EN的最小值.
等边△ABC的边长是8,AD⊥BC,E是BD的中点,M、N分别是AB、AD上的动点,求MN+EN的最小值. 如图所示,求∠A+∠B+∠C+∠D+∠E的度数.
如图所示,求∠A+∠B+∠C+∠D+∠E的度数.