题目内容
6.计算:(1)($\sqrt{2}$-1.414)0+($\frac{1}{3}$)-1-$\sqrt{3}$+2cos30°
(2)先化简,再求值:$\frac{x-2}{{x}^{2}-1}$$•\frac{x+1}{{x}^{2}-4x+4}$+$\frac{1}{x-1}$,其中x是从-1、0、1、2中选取一个合适的数.
分析 (1)分别根据0指数幂及负整数指数幂的计算法则、特殊角的三角函数值计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再选取合适的x的值代入进行计算即可.
解答 解:(1)原式=1+3-$\sqrt{3}$+2×$\frac{\sqrt{3}}{2}$
=1+3-$\sqrt{3}$+$\sqrt{3}$
=4;
(2)原式=$\frac{x-2}{(x+1)(x-1)}$•$\frac{x+1}{(x-2)^{2}}$+$\frac{1}{x-1}$
=$\frac{1}{(x-1)(x-2)}$+$\frac{1}{x-1}$
=$\frac{1+x-2}{(x-1)(x-2)}$
=$\frac{x-1}{(x-1)(x-2)}$
=$\frac{1}{x-2}$,
当x=0时,原式=-$\frac{1}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
14.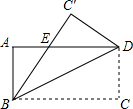 如图,矩形ABCD沿直线BD折叠,使点C落在点C处,BC交AD于点E,AD=8,AB=4,则BE的长为( )
如图,矩形ABCD沿直线BD折叠,使点C落在点C处,BC交AD于点E,AD=8,AB=4,则BE的长为( )
 如图,矩形ABCD沿直线BD折叠,使点C落在点C处,BC交AD于点E,AD=8,AB=4,则BE的长为( )
如图,矩形ABCD沿直线BD折叠,使点C落在点C处,BC交AD于点E,AD=8,AB=4,则BE的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 2$\sqrt{3}$ |
1.下列图形中,是轴对称图形但不是中心对称图形的是( )
| A. | 等边三角形 | B. | 正六边形 | C. | 正方形 | D. | 圆 |
15.和睦社区一次歌唱比赛共500名选手参加,比赛分数均大于或等于60且小于100,分数段的频率分布情况如表所示(其中每个分数段可包括最小值,不包括最大值),结合表中的信息,可得比赛分数在80~90分数段的选手有150名.
| 分数段 | 60~70 | 70~80 | 80~90 | 90~100 |
| 频率 | 0.2 | 0.25 | 0.25 |
12.对于任意实数k关于x的方程x2-2kx+k2-1=0根的情况为( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
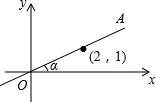 如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是$\frac{1}{2}$.
如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是$\frac{1}{2}$.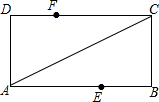 如图,矩形ABCD中,AB=2,BC=4,将矩形沿对角线AC翻折,使AB边上的点E与CD边上的点F重合,则AE的长是2.5.
如图,矩形ABCD中,AB=2,BC=4,将矩形沿对角线AC翻折,使AB边上的点E与CD边上的点F重合,则AE的长是2.5.