题目内容
19.已知抛物线y=(m-1)x2-$\sqrt{5{m}^{2}-5m}$x+m-1.(1)若抛物线的对称轴为y轴,求m的值.
(2)若抛物线的顶点在x轴上,求m的值.
分析 (1)由抛物线的对称轴为y轴,可知对称轴为x=0,从而可以求得m的值;
(2)由抛物线的顶点在x轴上,可知抛物线顶点的纵坐标为0,从而可以求得m的值.
解答 解:(1)∵抛物线y=(m-1)x2-$\sqrt{5{m}^{2}-5m}$x+m-1,抛物线的对称轴为y轴,
∴对称轴x=$\frac{-\sqrt{5{m}^{2}-5m}}{-2×(m-1)}$=0,m-1≠0.
解得m=0.
即抛物线的对称轴为y轴,m的值为0.
(2))∵抛物线y=(m-1)x2-$\sqrt{5{m}^{2}-5m}$x+m-1,抛物线的顶点在x轴上,
∴$\frac{4×(m-1)×(m-1)-(-\sqrt{5{m}^{2}-5m})^{2}}{4×(m-1)}$=0,m-1≠0.
解得m=-4.
即抛物线的顶点在x轴上,m的值为-4.
点评 本题考查二次函数的性质,解题的关键是明确顶点在y轴上时,顶点的横坐标为0,顶点在x轴上时,顶点的纵坐标为0.

练习册系列答案
相关题目
9.把一条弯曲的公路改成直道,可以缩短路程,用几何知识解释其道理正确的是( )
| A. | 两点确定一条直线 | B. | 直线可以向两方无限延伸 | ||
| C. | 两点之间线段最短 | D. | 一条线段可以分成两条相等的线段 |
7.下列各式可用完全平方公式计算的是( )
| A. | (2a-3b)(3b-2a) | B. | (2a-3b)(-3b+2a) | C. | (-2m+n)(2m+n) | D. | (2m+n)(2n-m) |
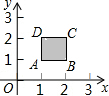 有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A(1,1)、B(2,1)、C(2,2)、D(1,2),用信号枪沿直线y=2x+b发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围为-3≤b≤0.
有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A(1,1)、B(2,1)、C(2,2)、D(1,2),用信号枪沿直线y=2x+b发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围为-3≤b≤0.