题目内容
5. “描点法”作图是探究函数图象的基本方法,小明同学用“描点法”画二次函数y=ax2+bx+c的图象时,列了如下表格:
“描点法”作图是探究函数图象的基本方法,小明同学用“描点法”画二次函数y=ax2+bx+c的图象时,列了如下表格:| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -3 | 1 | 3 | 1 | … |
(1)二次函数y=ax2+bx+c与y轴交点坐标是(0,1);该抛物线的开口向下;当x=4时,二次函数y=ax2+bx+c的值为-3
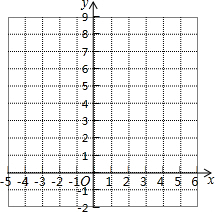
(2)小明还用“描点法”研究了函数y=$\frac{4}{{x}^{2}}$的图象和性质,请你在下面的方格纸中帮小明画出函数y=$\frac{4}{{x}^{2}}$的图象.借助所画的图象,回答下面问题:
①函数y=$\frac{4}{{x}^{2}}$的图象关于y轴对称;
②当x>0时,y随x的增大而增大;当x<0时,y随x的增大而减小.
分析 (1)当x=0时,即可得出二次函数y=ax2+bx+c与y轴交点坐标,再由a的符号得出抛物线的开口方向,根据抛物线的对称性,即可得出答案;
(2)图象如图,①根据图象即可得出答案;②第一象限内,y随x的增大而增大;第二象限内,y随x的增大而增大.
解答 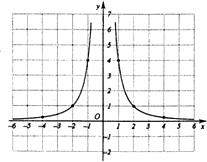 解:(1)当x=0时,y=1,
解:(1)当x=0时,y=1,
∴二次函数y=ax2+bx+c与y轴交点坐标是(0,1);
有点的坐标(0,1),(3,1),可得出对称轴x=$\frac{0+3}{2}$=$\frac{3}{2}$,
∵在对称左侧,y随x的增大而增大,
∴抛物线的开口向下,
当x=4和x=-1时,y的值相等,
∴x=4时y=-3;
(2)图象如图所示,
①函数y=$\frac{4}{{x}^{2}}$的图象关于y轴对称;
②当x>0时,y随x的增大而减小;
当x<0时,y随x的增大而增大;
故答案为(0,1),向下,-3,y轴,x>0,x<0.
点评 本题考查了二次函数的图象和性质,二次函数y=ax2+bx+c(a,b,c为常数,a≠0),当a>0时,在对称轴左侧y随x的增大而减小,在对称轴右侧y随x的增大而增大;当a<0时,在对称轴左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小.正比例函数中当k>0时,y随x的增大而增大,k<0时,y随x的怎大而减小.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
13.一元二次方程x2-2x-1=0,其解的情况正确的是( )
| A. | 有两个相等的实数解 | B. | 有两个不相等的实数解 | ||
| C. | 没有实数解 | D. | 不确定 |
10.对角线相等的正多边形是( )
| A. | 正方形 | B. | 正五边形 | ||
| C. | 正六边形 | D. | 正方形或正五边形 |
14.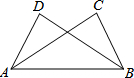 如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )
如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )
 如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )
如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )| A. | ∠D=∠C | B. | BD=AC | C. | ∠CAD=∠DBC | D. | AD=BC |
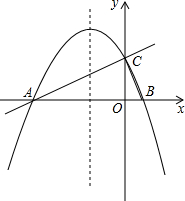 已知抛物线的解析式为y=-$\frac{1}{2}{x^2}-\frac{3}{2}$x+c.
已知抛物线的解析式为y=-$\frac{1}{2}{x^2}-\frac{3}{2}$x+c.