题目内容
20.将下列长度的三根木棒首尾顺次连接,不能组成直角三角形的是( )| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | C. | 6,8,10 | D. | 5,12,13 |
分析 分别计算出两个较小的边长的平方和,再计算出最长边的平方,根据规律的逆定理进行判断.
解答 解:∵12+($\sqrt{2}$)2=($\sqrt{3}$)2,
∴1,$\sqrt{2}$,$\sqrt{3}$能组成直角三角形;
∵($\sqrt{3}$)2+($\sqrt{4}$)2≠($\sqrt{5}$)2,
∴$\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$不能组成直角三角形;
∵62+82=102,
∴6,8,10能组成直角三角形;
∵52+122=132,
∴5,12,13能组成直角三角形.
故选:B.
点评 本题考查的是勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形

练习册系列答案
相关题目
11.如图,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.若前m个格子中所填整数之和是2014,则m的值为( )
| 9 | a | b | c | -5 | 1 | … |
| A. | 2015 | B. | 1008 | C. | 1208 | D. | 2008 |
8.下列各对数中,数值相等的是( )
| A. | (2)3和(-3)2 | B. | -32和(-3)2 | C. | -33和(-3)3 | D. | -3×23和(-3×2)3 |
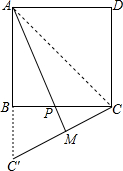 在边长为1的正方形ABCD中,点P是边BC上一点(点P不与点B,点C重合),点C关于直线AP的对称点为C′.
在边长为1的正方形ABCD中,点P是边BC上一点(点P不与点B,点C重合),点C关于直线AP的对称点为C′.