题目内容
17.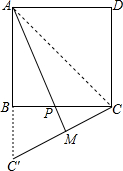 在边长为1的正方形ABCD中,点P是边BC上一点(点P不与点B,点C重合),点C关于直线AP的对称点为C′.
在边长为1的正方形ABCD中,点P是边BC上一点(点P不与点B,点C重合),点C关于直线AP的对称点为C′. (1)如果C′落在线段AB的延长线上,
①求∠BAP的度数;
②求线段BP的长度;
(2)设直线AP与CC′的交点为M,求证:BM⊥DM.
分析 (1)①由正方形的性质得出AB=BC=1,∠ABC=90°,∠BAC=$\frac{1}{2}$∠BAD=45°,由对称的性质得出∠BAP=∠CAP=$\frac{1}{2}$∠BAC即可;
②由勾股定理求出AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{2}$,由角平分线的性质定理即可求出BP的长度;
(2)连接BM,先证明B、M、C、A四点共圆,得出∠AMD=∠ACD=45°,再证明A、M、C、D四点共圆,得出∠AMD=∠ACD=45°,得出∠BMD=90°即可.
解答 (1)解:①∵四边形ABCD是正方形,
∴AB=BC=1,∠ABC=90°,∠BAC=$\frac{1}{2}$∠BAD=45°,
由对称的性质得:∠BAP=∠CAP=$\frac{1}{2}$∠BAC=22.5°;
②由勾股定理得:AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{2}$,
由①得:AP是∠BAC的平分线,
∴$\frac{BP}{CP}=\frac{AB}{AC}$,
即$\frac{BP}{1-BP}=\frac{1}{\sqrt{2}}$,
解得:BP=$\sqrt{2}$-1;
(2)证明:如图所示: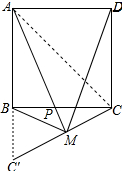
∵∠ABC=∠AMC=90°,
∴B、M、C、A四点共圆,
∴∠AMD=∠ACD=45°,
∵∠AMC=∠ADC=90°,
∴A、M、C、D四点共圆,
∴∠AMD=∠ACD=45°,
∴∠BMD=90°,
∴BM⊥DM.
点评 本题考查了正方形的性质、勾股定理、对称的性质、角平分线的性质定理、四点共圆、圆周角定理等知识;本题综合性强,有一定难度.

练习册系列答案
相关题目
20.将下列长度的三根木棒首尾顺次连接,不能组成直角三角形的是( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | C. | 6,8,10 | D. | 5,12,13 |
7.如果a+b>0,且ab<0,那么( )
| A. | a>0,b>0 | B. | a<0,b<0 | ||
| C. | a、b异号 | D. | a、b异号且正数的绝对值较大 |
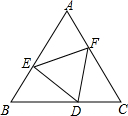 如图,边长为2的正三角形DEF的三个顶点恰好在边长为3的正三角形ABC的各边上,则三角形AEF的内切圆的半径为$\frac{\sqrt{3}}{6}$.
如图,边长为2的正三角形DEF的三个顶点恰好在边长为3的正三角形ABC的各边上,则三角形AEF的内切圆的半径为$\frac{\sqrt{3}}{6}$.