题目内容
9. 如图,在矩形ABCD中,对角线AC、BD相交于点O,AE平分∠BAD,交BC于点E,已知∠CAE=15°,AB=2cm,求∠BOE的度数及矩形ABCD的面积.
如图,在矩形ABCD中,对角线AC、BD相交于点O,AE平分∠BAD,交BC于点E,已知∠CAE=15°,AB=2cm,求∠BOE的度数及矩形ABCD的面积.
分析 先证明OB=BE,△OAB是等边三角形,得出OB=AB=2,∠ABO=60°,根据等腰三角形的性质求出∠BOE,再运用勾股定理求出AD,矩形的面积=AB•AD.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,OB=$\frac{1}{2}$BD,OA=$\frac{1}{2}$AC,AC=BD,
∴OA=OB,
∵AE平分∠BAD,
∴∠BAE=45°,
∴BE=AB=2,∠OAB=∠BAE+∠CAE=60°,
∴OB=BE,△OAB是等边三角形,
∴OB=AB=2,∠ABO=60°,
∴∠OBE=30°,
∴∠BOE=$\frac{1}{2}$(180°-30°)=75°,
∵BD=2OB=4,
∴AD=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴矩形ABCD的面积=AB•AD=2×2$\sqrt{3}$=4$\sqrt{3}$.
点评 本题考查了矩形的性质、等边三角形的判定与性质、等腰三角形的性质、勾股定理的运用;熟练掌握矩形和等边三角形的性质是解决问题的关键.

练习册系列答案
相关题目
19. 如图,∠1=30°,则射线OA表示为( )
如图,∠1=30°,则射线OA表示为( )
 如图,∠1=30°,则射线OA表示为( )
如图,∠1=30°,则射线OA表示为( )| A. | 南偏西60° | B. | 南偏西30° | C. | 南偏东60° | D. | 南偏东30° |
 如图,点B、E、F、C在一条直线上,AB=DE=10,AC=DF,BE=CF=CE.
如图,点B、E、F、C在一条直线上,AB=DE=10,AC=DF,BE=CF=CE.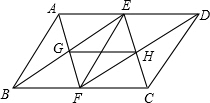 如图:E、F分别是?ABCD的对边AD、BC的中点,AF、BE交于点G,EC与DF交于H.
如图:E、F分别是?ABCD的对边AD、BC的中点,AF、BE交于点G,EC与DF交于H. 如图,在△ABC中,∠A=90°,E是AC上一点,ED⊥BC,DF⊥AB,垂足分别为D、F,若∠AED=140°,求∠C和∠BDF的度数.
如图,在△ABC中,∠A=90°,E是AC上一点,ED⊥BC,DF⊥AB,垂足分别为D、F,若∠AED=140°,求∠C和∠BDF的度数.