题目内容
已知α是锐角且tan α= ,则sin α+cos α= .
,则sin α+cos α= .
 .
.
【解析】
试题分析:如图所示,因为 ,所以可设BC=3,AC=4,则AB=5,所以
,所以可设BC=3,AC=4,则AB=5,所以 ,
, ,所以sin α+cos α=
,所以sin α+cos α= .
.
故答案为: .
.

考点:锐角三角形函数的应用.
考点分析: 考点1:解直角三角形 (1)解直角三角形的定义在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.
(2)解直角三角形要用到的关系
①锐角直角的关系:∠A+∠B=90°;
②三边之间的关系:a2+b2=c2;
③边角之间的关系:
sinA=∠A的对边斜边=ac,cosA=∠A的邻边斜边=bc,tanA=∠A的对边∠A的邻边=ab.
(a,b,c分别是∠A、∠B、∠C的对边) 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

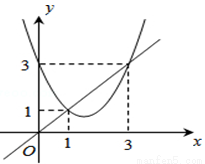
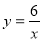 的图像上的是( )
的图像上的是( )
 _______.
_______.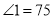 ,则
,则 的大小是( ).
的大小是( ).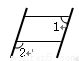
 = .
= .