题目内容
已知ax2+bx+1与3x+1的积不含x3的项,也不含x的项,那么a= ,b= .
0,-3.
【解析】
试题分析:由题意列出算式,利用多项式乘以多项式法则计算,合并后令三次项与一次项系数为0,即可求出a与b的值.
试题解析:根据题意列得:(ax2+bx+1)(3x+1)=3ax3+(a+3b)x2+(b+3)x+1,
∵不含x3的项,也不含x的项,
∴3a=0,b+3=0,
则a=0,b=-3.
考点:多项式乘多项式.
考点分析: 考点1:整式加减 整式的加减:其实质是去括号和合并同类项,其一般步骤为:
(1)如果有括号,那么先去括号;
(2)如果有同类项,再合并同类项。
注:整式加减的最后结果中不能含有同类项,即要合并到不能再合并为止。
整式的加减即合并同类项。把同类项相加减,不能计算的就直接拉下来。
合并同类项时要注意以下三点:
①要掌握同类项的概念,会辨别同类项,并准确地掌握判断同类项的两条标准.字母和字母指数;
②明确合并同类项的含义是把多项式中的同类项合并成一项,经过合并同类项,式的项数会减少,达到化简多项式的目的;
③“合并”是指同类项的系数的相加,并把得到的结果作为新的系数,要保持同类项的字母和字母的指数不变。
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,则sin α+cos α= .
,则sin α+cos α= .
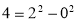 ,
,  ,
,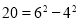 ,因此4,12,20都是“神秘数”
,因此4,12,20都是“神秘数”