题目内容
三角形的三边长分别为3、m、5,化简 _______.
_______.
2m-10.
【解析】
试题分析:根据三角形的三边关系可知, ,根据m的取值范围对代数式进行化简,原式=m-2-8+m=2m-10.
,根据m的取值范围对代数式进行化简,原式=m-2-8+m=2m-10.
故答案为:2m-10.
考点:三角形的三边关系;二次根式的化简.
考点分析: 考点1:三角形 (1)三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.组成三角形的线段叫做三角形的边.
相邻两边的公共端点叫做三角形的顶点.
相邻两边组成的角叫做三角形的内角,简称三角形的角.
(2)按边的相等关系分类:不等边三角形和等腰三角形(底和腰不等的等腰三角形、底和腰相等的等腰三角形即等边三角形).
(3)三角形的主要线段:角平分线、中线、高.
(4)三角形具有稳定性. 考点2:二次根式 二次根式:
我们把形如
 叫做二次根式。
叫做二次根式。二次根式必须满足:
含有二次根号“
 ”;
”;被开方数a必须是非负数。
确定二次根式中被开方数的取值范围:
要是二次根式
 有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。
二次根式性质:
有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。
二次根式性质:(1)a≥0 ;
 ≥0 (双重非负性 );
≥0 (双重非负性 );(2)
 ;
;(3)

0(a=0);
(4)
 ;
;(5)
 。
二次根式判定:
。
二次根式判定:①二次根式必须有二次根号,如
 ,
, 等;
等;②二次根式
 中,被开方数a可以是具体的一个数,也可以是代数式;
中,被开方数a可以是具体的一个数,也可以是代数式;③二次根式定义中a≥0 是定义组成的一部分,不能省略;
④二次根式
 是一个非负数;
是一个非负数;⑤二次根式与算术平方根有着内在的联系,
 (a≥0 )就表示a的算术平方根。
(a≥0 )就表示a的算术平方根。二次根式的应用:
主要体现在两个方面:
(1)利用从特殊到一般,在由一般到特殊的重要思想方法,解决一些规律探索性问题;
(2)利用二次根式解决长度、高度计算问题,根据已知量,求出一些长度或高度,或设计省料的方案,以及图形的拼接、分割问题。这个过程需要用到二次根式的计算,其实就是化简求值。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目


 ,则sin α+cos α= .
,则sin α+cos α= . :y=
:y= x
x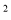 +4x+4
+4x+4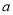 (0<
(0<

 ,抛物线C
,抛物线C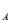 ),B(0,y
),B(0,y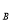 ),C(-1,y
),C(-1,y )三点均在C
)三点均在C



