题目内容
3. 已知如图,△ABC中,∠C=90°,AB=10,BC=6,
已知如图,△ABC中,∠C=90°,AB=10,BC=6,(1)计算AC的长度;
(2)计算AB边上的中线CD的长度.
(3)计算AB边上的高CE的长度.
分析 (1)在Rt△ABC中,根据勾股定理可求得AC的长;
(2)在Rt△ABC中,根据斜边上的中线等于斜边的一半,即可得出CD的长;
(3)在Rt△ABC中,根据面积法即可得出CE的长.
解答 解:(1)∵△ABC中,∠C=90°,AB=10,BC=6,
∴由勾股定理得,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8;
(2)∵Rt△ABC中,∠C=90°,AB=10,
∴AB边上的中线CD=$\frac{1}{2}$AB=5;
(3)∵Rt△ABC中,∠C=90°,AB=10,BC=6,AC=8,CE⊥AB,
∴$\frac{1}{2}$×AB×CE=$\frac{1}{2}$×AC×BC,
即10×CE=8×6,
∴CE=4.8
点评 本题主要考查了直角三角形的性质的综合应用,解题时注意:在直角三角形中,斜边上的中线等于斜边的一半;在一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
17. 若有理数m,n在数轴上的位置如图所示,下列各式正确的是( )
若有理数m,n在数轴上的位置如图所示,下列各式正确的是( )
 若有理数m,n在数轴上的位置如图所示,下列各式正确的是( )
若有理数m,n在数轴上的位置如图所示,下列各式正确的是( )| A. | -m<0 | B. | m+n>0 | C. | -n<|m| | D. | mn>0 |
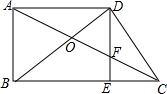 如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,对角线AC,BD相交于点O,过D作DE⊥BC,交AC于点F.
如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,对角线AC,BD相交于点O,过D作DE⊥BC,交AC于点F.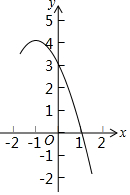 已知抛物线y=-x2+bx+c的部分图象如图所示.
已知抛物线y=-x2+bx+c的部分图象如图所示.