题目内容
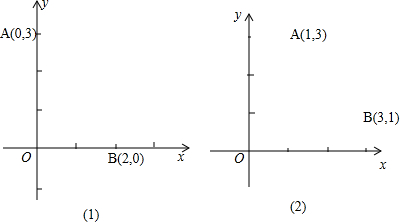
3.(1)如图(1),点C的坐标为(3,y).使△ABC的周长最短.求y的值.(2)如图(2).在x轴上有一点C,在y轴上有一点D.使AD+CD+BC值最小.求直线CD的解析式及点C、D坐标.
分析 作出点A关于直线x=3的对称点A′,连接A′B交直线x=3与点C,先求得BA′的解析式,然后将x=3代入直线BA′的解析式,从而可求得y的值;
解答 解:(1)作A关于x=3的对称点A′,连接A′B交直线x=3与点C.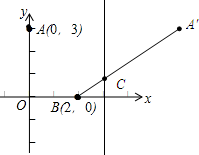
∵点A与点A′关于x=3对称,
∴AC=A′C.
∴AC+BC=A′C+BC.
当点B、C、A′在同一条直线上时,A′C+BC有最小值,即△ABC的周长有最小值.
∵点A与点A′关于x=3对称,
∴点A′的坐标为(6,3).
设直线BA′的解析式y=kx+b,将点B和点A′的坐标代入得:$\left\{\begin{array}{l}{2k+b=0}\\{6k+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=-\frac{3}{2}}\end{array}\right.$.
∴y=$\frac{3}{4}x-\frac{3}{2}$.
将x=3代入函数的解析式得y=$\frac{3}{4}$.
∴y的值为$\frac{3}{4}$;
(2)作A关于y轴的对称点A′(-1,3),B关于x轴的对称点B′(3,-1),
易知直线A′B′的解析式为y=-x+2,直线交x轴于C,交y轴于D,此时AD+CD+BC值最小,
易知C(2,0),D(0,2).
点评 本题主要考查的是轴对称路径最短、一次函数,明确当点B、C、A′在同一条直线上时,A′C+BC有最小值是解题的关键.

练习册系列答案
相关题目
14.某饮料加工厂从所生产的瓶装饮料中抽取了50瓶检查质量,质量超过标准质量的用正数表示,质量低于标准质量的用负数表示,结果记录如表:
(1)这50瓶饮料平均每瓶的质量比每瓶的标准质量多多少克?
(2)若这种饮料每瓶的标准质量是400克,求这50瓶饮料的总质量.
| 与标准质量的偏差(单位:克) | -7 | -6 | -1 | 0 | 5 | 10 |
| 瓶数 | 4 | 6 | 10 | 13 | 9 | 8 |
(2)若这种饮料每瓶的标准质量是400克,求这50瓶饮料的总质量.
11.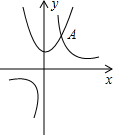 如图,抛物线y=x2+2与双曲线y=$\frac{k}{x}$的交点A的横坐标是2,则关于x的不等式$\frac{k}{x}$+x2+2<0的解是( )
如图,抛物线y=x2+2与双曲线y=$\frac{k}{x}$的交点A的横坐标是2,则关于x的不等式$\frac{k}{x}$+x2+2<0的解是( )
 如图,抛物线y=x2+2与双曲线y=$\frac{k}{x}$的交点A的横坐标是2,则关于x的不等式$\frac{k}{x}$+x2+2<0的解是( )
如图,抛物线y=x2+2与双曲线y=$\frac{k}{x}$的交点A的横坐标是2,则关于x的不等式$\frac{k}{x}$+x2+2<0的解是( )| A. | 0<x<2 | B. | -2<x<0 | C. | x>2 | D. | x<-2 |
 a,b表示如图数轴上的两个数,
a,b表示如图数轴上的两个数,