题目内容
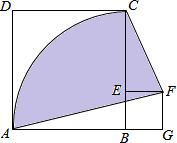 如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画AC,连AF、CF,则图中阴影部分面积为( )
如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画AC,连AF、CF,则图中阴影部分面积为( )| A、2π | B、4π |
| C、4π-2 | D、6π |
考点:整式的混合运算,扇形面积的计算
专题:
分析:根据正方形的性质得出∠G=∠ABC=∠CEF=90°,AB=B=4,EF=BE=GF=BG,设EF=BE=GF=BG=a,则阴影部分的面积S=S扇形BAC+S正方形EFGB+S△CEF-S△AGF,代入求出即可.
解答:解:∵四边形ABCD和四边形EFGB是正方形,
∴∠G=∠ABC=∠CEF=90°,AB=B=4,EF=BE=GF=BG,
设EF=BE=GF=BG=a,
则阴影部分的面积S=S扇形BAC+S正方形EFGB+S△CEF-S△AGF
=
+a2+
•a•(4-a)-
•(4+a)a
=4π,
故选B.
∴∠G=∠ABC=∠CEF=90°,AB=B=4,EF=BE=GF=BG,
设EF=BE=GF=BG=a,
则阴影部分的面积S=S扇形BAC+S正方形EFGB+S△CEF-S△AGF
=
| 90π×42 |
| 360 |
| 1 |
| 2 |
| 1 |
| 2 |
=4π,
故选B.
点评:本题考查了整式的混合运算的应用,解此题的关键是能表示出阴影部分的面积.

练习册系列答案
相关题目
不改变原式的值,将6-(+3)-(-7)+(-2)中的减法改成加法并写成省略加号和括号的形式是( )
| A、-6-3+7-2 |
| B、6-3-7-2 |
| C、6-3+7-2 |
| D、6-3-7-2 |
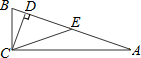 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,点E是AB中点,AB=10,则线段DE的长度为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,点E是AB中点,AB=10,则线段DE的长度为( )