题目内容
1.甲、乙两人练习跑步,若乙先跑8米,则甲跑4分钟可追上乙;若乙先跑2分钟,则甲跑5分钟可追上乙.若设甲的速度为x米/分,乙的速度为y米/分,则下列列出的方程组中正确的是( )| A. | $\left\{\begin{array}{l}{4x=4y+8}\\{5x=2y+5y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{4x+8=4y}\\{5x=2y+5y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{4x=4y+8}\\{5x=5y-2y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{4x+8=4y}\\{5x+2y=5y}\end{array}\right.$ |
分析 根据乙先跑8米,则甲跑4分钟就可以追上乙,得方程4x=4y+8;根据乙先跑2分钟,则甲跑5分钟就可追上乙,得方程5x=5y+2y.由此列出方程组即可.
解答 解:若设甲的速度为x米/分,乙的速度为y米/分,由题意得
$\left\{\begin{array}{l}{4x=4y+8}\\{5x=5y+2y}\end{array}\right.$.
故选:A.
点评 此题考查由实际问题抽象出二元一次方程组,掌握追及问题中的等量关系:甲跑的路程=乙跑的路程是解决问题的关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
16.下列各组数都是无理数的是( )
| A. | 0.2,$\sqrt{3}$ | B. | $\frac{\sqrt{2}}{3}$,$\sqrt{4}$ | C. | $\frac{4}{5}$,0 | D. | 2$\sqrt{3}$,$\sqrt{5}$+$\sqrt{3}$ |
13.如果一个多边形的每个内角都相等,且内角和为1440°,则这个多边形的外角是( )
| A. | 30° | B. | 36° | C. | 40° | D. | 45° |
11. 如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为14cm,则四边形ABFD的周长为( )
如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为14cm,则四边形ABFD的周长为( )
 如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为14cm,则四边形ABFD的周长为( )
如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为14cm,则四边形ABFD的周长为( )| A. | 14cm | B. | 17cm | C. | 20cm | D. | 23cm |
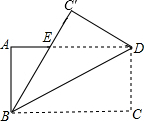 如图,将矩形ABCD沿对角线BD折叠,使点C与C′重合.若AB=3,则C′D的长为3.
如图,将矩形ABCD沿对角线BD折叠,使点C与C′重合.若AB=3,则C′D的长为3.