题目内容
10.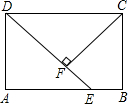 如图,四边形ABCD是矩形,E是AB上一点,且DE=AB,过点C作CF⊥DE,垂足为E.
如图,四边形ABCD是矩形,E是AB上一点,且DE=AB,过点C作CF⊥DE,垂足为E.(1)猜想:AD与CF的大小关系;
(2)请证明(1)中的结论.
分析 (1)猜想:AD=CF,根据全等三角形的性质得出即可;
(2)根据矩形的性质得出AB=CD,∠A=90°,DC∥AB,求出∠CDF=∠DEA,∠CFD=∠A=90°,CD=DE,根据AAS推出△AED≌△FDC,根据全等三角形的性质得出即可.
解答 解:(1)AD=CF;
(2)证明:∵四边形ABCD是矩形,
∴AB=CD,∠A=90°,DC∥AB,
∴∠CDF=∠DEA,
∵CF⊥DE,
∴∠CFD=∠A=90°,
∵AB=CD,AB=DE,
∴CD=DE,
在△AED和△FDC中,
$\left\{\begin{array}{l}{∠DEA=∠CDF}\\{∠A=∠CFD}\\{DE=DC}\end{array}\right.$,
∴△AED≌△FDC(AAS),
∴AD=CF.
点评 本题考查了矩形的性质,全等三角形的性质和判定,平行线的性质的应用,解此题的关键是能求出证△AED和△FDC全等的三个条件,难度适中.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
20.我们学习了圆周角定理,回顾学习过程,在探索同弧所对的圆周角和圆心角的关系时,主要体现的数学思想是( )
| A. | 转化 | B. | 数形结合 | C. | 演绎 | D. | 分类讨论 |
 已知a,b,c在数轴上对应点的位置如图所示,化简:|a|-|a+b|-$\sqrt{(c-a)^{2}}$+|b-c|.
已知a,b,c在数轴上对应点的位置如图所示,化简:|a|-|a+b|-$\sqrt{(c-a)^{2}}$+|b-c|. 在Rt△ABC中,∠C=90°,AB=3BC,AC=3$\sqrt{2}$,求AB、BC的长.
在Rt△ABC中,∠C=90°,AB=3BC,AC=3$\sqrt{2}$,求AB、BC的长.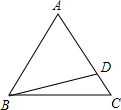 如图所示,在△ABC中,AB=AC,点D在AC上(不与A,C重合),BD=AB,求∠A的取值范围.
如图所示,在△ABC中,AB=AC,点D在AC上(不与A,C重合),BD=AB,求∠A的取值范围.