题目内容
16．抛物线y=4x2-11x-3与x轴的交点为（-$\frac{1}{4}$，0）或（3，0），与y轴的交点为（0，-3）．分析 在函数解析式中令y=0，解方程求得x即可求得与x轴的横坐标；令y=0，即可求得与y轴交点的纵坐标．
解答 解：在y=4x2-11x-3中令y=0，则4x2-11x-3=0，
解得：x=-$\frac{1}{4}$或3，
则与x轴的交点坐标是（-$\frac{1}{4}$，0）或（3，0）；
在y=4x2-11x-3中令x=0，解得y=-3，则与y轴的交点是（0，-3）．
故答案是：（-$\frac{1}{4}$，0）或（3，0）；（0，-3）．
点评 本题考查了函数图象与x轴、y轴交点的求法，求与x轴交点时令y=0求得横坐标，求与y轴的交点时，令x=0求纵坐标．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
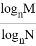（a＞0，a≠1，N＞0，N≠1，M＞0）．例如：log223=3，log25=
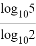，则log1001000=_____．
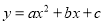经过点A(5,0)，B(-3,0),C(0,4). 
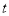（秒)(0＜
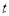＜7)，△PQB的面积记为S.
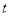的函数关系式；
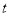为何值时，S有最大值，最大值是多少？
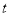值，使得△PQB是直角三角形?若存在，请直接写出
的值；若不存在，请说明理由.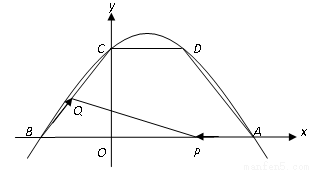
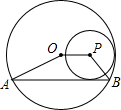如图，⊙P内切于⊙O，⊙O的弦AB与⊙P相切，且AB∥OP，若⊙O的半径为3，⊙P的半径为1，则四边形ABPO的面积为2$+2\sqrt{2}$．
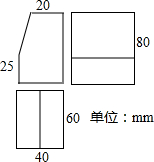已知一个几何体的三视图如图所示．
4．求一个数的立方根，有些数可以直接求得，如$\root{3}{8}$，有些数则不能直接求得，如$\root{3}{5}$，但可以通过计算器求得．还有一种方法可以通过一组数的内在联系，运用规律求得，请同学们观察下表：
（1）表中所给的信息中，你能发现什么规律？（请将规律用文字表达出来）
（2）运用你发现的规律，探究下列问题：
已知$\root{3}{2.5}$≈1.36，求下列各数的立方根：
①0.0025； ②2500000．
| n | 8 | 0.008 | 0.000008 | 8000 | 8000000 | … |
| $\root{3}{n}$ | 2 | 0.2 | 0.02 | 20 | 200 | … |
（2）运用你发现的规律，探究下列问题：
已知$\root{3}{2.5}$≈1.36，求下列各数的立方根：
①0.0025； ②2500000．