题目内容
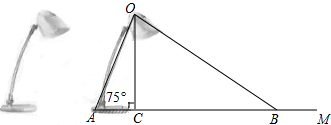
16.问题:如图(1),点F、E分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BF、EF、DE之间的数量关系.(1)【发现证明】
如图1,小聪把△ADE绕点A顺时针旋转90°得到△ABG,从而发现EF=BF+ED.请完成下列填空.
解:由旋转可得:AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°.
因此,点G,B,F在同一条直线上.∵∠EAF=45°∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°∵∠1=∠2∴∠1+∠3=45°,即∠GAF=∠EAF.
又AG=AE,AF=AF∴△GAF≌△EAF∴GF=EF,故DE+BF=EF
(2)【类比延伸】
如图(2),四边形ABCD中,∠BAD=90°,AB=AD,∠B+∠D=180°,点F、E分别在边BC、CD上,则当∠EAF与∠BAD满足∠EAF=$\frac{1}{2}$∠BAD关系时,仍有EF=BF+DE.
(3)【探究应用】
如图(3),在某公园的同一水平面上,通道AB、AC、BC、AN、AM构成了等腰Rt△ABC,已知∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=$\sqrt{5}$米,CN=3$\sqrt{2}$米,求通道MN的长.
分析 (1)根据全等三角形的判定定理证明△GAF≌△EAF,根据全等三角形的性质解答即可;
(2)把△ABF绕点A逆时针旋转90°至△ADG,可使AB与AD重合,证明△AFE≌△AGE即可;
(3)把△ABM绕点A逆时针旋转90°得到△ACG,连接NG,根据勾股定理得到NG2=NC2+CG2,由(1)得△ANM≌△ANG,得到NG=NM,代入已知数据计算即可.
解答 解:(1)由旋转可得:AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上,
∵∠EAF=45°,
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°,
∵∠1=∠2,
∴∠1+∠3=45°,即∠GAF=∠EAF,
又AG=AE,AF=AF,
∴△GAF≌△EAF,
∴GF=EF,故DE+BF=EF;
(2)当∠EAF与∠BAD满足∠EAF=$\frac{1}{2}$∠BAD关系时,仍有EF=BF+DE.
如图2,∵AB=AD,
∴把△ABF绕点A逆时针旋转90°至△ADG,可使AB与AD重合,
∴∠BAF=∠DAG,
∵∠EAF=$\frac{1}{2}$∠BAD,
∴∠EAF=∠EAG,
∵∠ADC+∠B=180°,
∴∠EDG=180°,点E、D、G共线,
在△AFE和△AGE中,
$\left\{\begin{array}{l}{AD=AG}\\{∠FAE=∠GAE}\\{AE=AE}\end{array}\right.$,
∴△AFE≌△AGE,
∴GE=EF,即EF=BF+DE;
(3)如图3,把△ABM绕点A逆时针旋转90°得到△ACG,连接NG,
则∠ACG=∠ABM,
∴∠NCG=90°,
∴NG2=NC2+CG2,
由(1)得△ANM≌△ANG,
∴NG=NM,又CG=BM,
∴NM2=NC2+BM2=($\sqrt{5}$)2+(3$\sqrt{2}$)2=23,
∴通道MN的长为$\sqrt{23}$.
点评 本题考查的是全等三角形的判定和性质、折叠的性质、勾股定理的应用,掌握翻转变换的性质、灵活运用勾股定理是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 下列选项中,如图所示的圆柱的三视图画法正确的是( )
下列选项中,如图所示的圆柱的三视图画法正确的是( )| A. |  | B. |  | C. |  | D. |  |
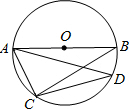 如图,AB是⊙O的直径,∠ADC=30°,OA=2,则AC的长为( )
如图,AB是⊙O的直径,∠ADC=30°,OA=2,则AC的长为( )| A. | 2 | B. | 4 | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |
| A. | $\frac{16}{27}$ | B. | $\frac{9}{8}$ | C. | $\frac{8}{27}$ | D. | $\frac{27}{16}$ |
| A. | 144 | B. | 96 | C. | 24 | D. | 12 |