题目内容
12．如图为放置在水平桌面上的台灯的平面示意图，灯臂AO长为40cm，与水平面所形成的夹角∠OAM为75°．由光源O射出的边缘光线OC，OB与水平面所形成的夹角∠OCA，∠OBA分别为90°和30°，求该台灯照亮水平面的宽度BC（不考虑其他因素，结果精确到0.1cm．温馨提示：sin75°≈0.97，cos75°≈0.26，$\sqrt{3}≈1.73$）．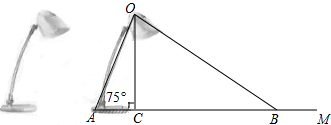
分析 根据sin75°=$\frac{OC}{OA}$=$\frac{OC}{40}$，求出OC的长，根据tan30°=$\frac{OC}{BC}$，再求出BC的长，即可求解．
解答 解：在直角三角形ACO中，sin75°=$\frac{OC}{OA}$=$\frac{OC}{40}$≈0.97，
解得OC≈38.8，
在直角三角形BCO中，tan30°=$\frac{OC}{BC}$=$\frac{38.8}{BC}$≈$\frac{1.73}{3}$，
解得BC≈67.3．
答：该台灯照亮水平面的宽度BC大约是67.3cm．
点评 此题主要考查了解直角三角形的应用，熟练应用锐角三角函数关系是解题关键．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
2．下列几何体中，主视图和俯视图都为矩形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
如图，点A，B在反比例函数y=$\frac{k}{x}$（k＞0）的图象上，AC⊥x轴，BD⊥x轴，垂足C，D分别在x轴的正、负半轴上，CD=k，已知AB=2AC，E是AB的中点，且△BCE的面积是△ADE的面积的2倍，则k的值是$\frac{3\sqrt{7}}{2}$．
20．
如图所示，直线AB、CD被直线EF所截，若AB∥CD，∠1=100°，则∠2的大小是（ ）
如图所示，直线AB、CD被直线EF所截，若AB∥CD，∠1=100°，则∠2的大小是（ ）| A． | 10° | B． | 50° | C． | 80° | D． | 100° |
17．
如图是某几何体的三视图，则该几何体可能是（ ）
如图是某几何体的三视图，则该几何体可能是（ ）| A． | 圆柱 | B． | 圆锥 | C． | 球 | D． | 长方体 |
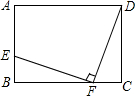已知：如图，在矩形ABCD中，点E在边AB上，点F在边BC上，且BE=CF，EF⊥DF，求证：BF=CD．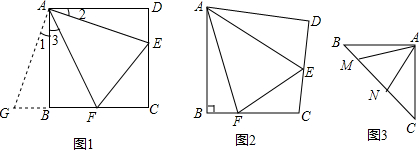
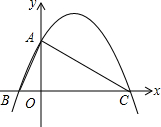已知，如图，在平面直角坐标系中，△ABC的边BC在x轴上，顶点A在y轴的正半轴上，OA=2，OB=1，OC=4．