题目内容
18.如果$\frac{1}{2}$|a+1|+|2b+1|=0,则$\frac{a-b}{a}$=$\frac{1}{2}$.分析 先根据非负数的性质求出a、b的值,再代入代数式进行计算即可.
解答 解:∵$\frac{1}{2}$|a+1|+|2b+1|=0,
∴a+1=0,2b+1=0,解得a=-1,b=-$\frac{1}{2}$,
∴$\frac{a-b}{a}$=$\frac{-1+\frac{1}{2}}{-1}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查的是非负数的性质,熟知个数的绝对值都是非负数,当几个数或式的绝对值相加和为0时,则其中的每一项都必须等于0是解答此题的关键.

练习册系列答案
相关题目
8.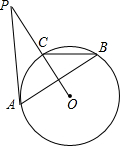 如图,PA与⊙O相切于点A,PO交⊙O于点C,点B是优弧CBA上一点,若∠P=26°,则∠ABC的度数为( )
如图,PA与⊙O相切于点A,PO交⊙O于点C,点B是优弧CBA上一点,若∠P=26°,则∠ABC的度数为( )
 如图,PA与⊙O相切于点A,PO交⊙O于点C,点B是优弧CBA上一点,若∠P=26°,则∠ABC的度数为( )
如图,PA与⊙O相切于点A,PO交⊙O于点C,点B是优弧CBA上一点,若∠P=26°,则∠ABC的度数为( )| A. | 26° | B. | 64° | C. | 32° | D. | 90° |
1.如果x=1是方程x2+ax+1=0的一个根,那么a的值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | -2 |
 如图,若∠3+∠2=180°,∠1=∠5,试说明d∥e.
如图,若∠3+∠2=180°,∠1=∠5,试说明d∥e.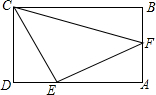 如图,在矩形ABCD中,△CEF为等腰直角三角形.
如图,在矩形ABCD中,△CEF为等腰直角三角形.