题目内容
18.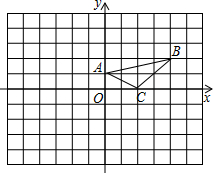 如图,在平面直角坐标系中,A(0,1),B(4,2),C(2,0).
如图,在平面直角坐标系中,A(0,1),B(4,2),C(2,0).(1)将△ABC沿y轴翻折得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕着点(-1,-1)旋转180°得到△A2B2C2,画出△A2B2C2;
(3)线段B2C2可以看成是线段B1C1绕着平面直角坐标系中某一点逆时针旋转得到,直接写出旋转中心的坐标为(-6,0).
分析 (1)利用关于y轴对称的点坐标特征写出点A1、B1、C1的坐标,然后描点即可;
(2)利用网格特点和旋转的性质画出点A1、B1、C1的对应点A2、B2、C2,从而得到△A2B2C2;
(3)作B1B2和C1C2的垂直平分线,它们相交于点P,则点P为旋转中心,然后写出P点坐标即可.
解答 解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;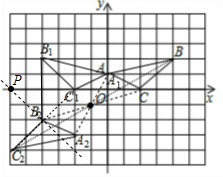
(3)如图,线段B2C2可以看成是线段B1C1绕着点P逆时针旋转270°得到,此时P点的坐标为(-6,0).
故答案为(-6,0).
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
相关题目
 如图,在四边形ABCD中,对角线AC、BD相交于点O,且AO=CO,BO=DO,要使四边形ABCD为矩形,则需添加的条件为∠DAB=90°(填一个即可).
如图,在四边形ABCD中,对角线AC、BD相交于点O,且AO=CO,BO=DO,要使四边形ABCD为矩形,则需添加的条件为∠DAB=90°(填一个即可).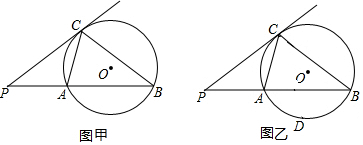
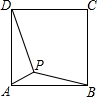 如图,点P是正方形ABCD内一点,PA=1,PD=$\sqrt{10}$,∠APB=135°,则PB的长为2$\sqrt{2}$.
如图,点P是正方形ABCD内一点,PA=1,PD=$\sqrt{10}$,∠APB=135°,则PB的长为2$\sqrt{2}$.
 如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,其中点B的坐标为(1,0),若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是-1<k<$\frac{1}{4}$.
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,其中点B的坐标为(1,0),若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是-1<k<$\frac{1}{4}$.