直角三角形的斜边长为8.内切圆的半径为1.则这个三角形的周长为( )A．21B．20C．19D．18 题目和参考答案——青夏教育精英家教网—

题目内容

13．直角三角形的斜边长为8，内切圆的半径为1，则这个三角形的周长为（　　）

A．

B．

C．

D．

分析首先根据题意画出图形，设AD=x，则BD=8-x，由切线长定理得AD=AF=x，BD=BE=8-x，可证明四边形OECF为正方形，则CE=CF=1，再由三角形的周长公式求出这个三角形周长．

解答解：如图所示：

设AD=x，则BD=8-x，
∵⊙O是△ABC内切圆，
∴AD=AF=x，BD=BE=8-x．
∵∠C=∠OFC=∠OEC=90°，OE=OF，
∴四边形OECF为正方形．
∴CE=CF=1．
∴这个三角形周长：2x+2（8-x）+2=18．
故选：D．

点评本题考查了三角形的内切圆和内心，以及切线长定理，方程思想与数形结合思想的应用是解题的关键．

练习册系列答案

相关题目

4．下列说法：
①在△ABC中，若∠A：∠B：∠C=3：4：5，则△ABC为直角三角形；
②已知直角三角形的面积为2，两直角边的比为1：2，则斜边长的平方为10；
③在Rt△ABC中，若两边长分别为3和4，则第三边长为5；
④已知等腰三角形的面积为12，底边上的高为4，则腰长为5．
其中正确结论的序号是（　　）

1．已知Rt△ABC的两边长分别为AB=4，BC=5，则AC=3或$\sqrt{41}$．

8．设y=ax²+bx+1（a≠0），y的最大值为1，则（　　）

18．

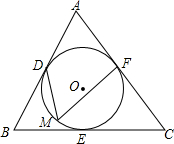如图，⊙O分别切△ABC的边AB、BC、CA于点D、E、F，∠B=70°，∠C=60°，M是$\widehat{DEF}$上的动点（与点D、E不重合），∠DMF的大小一定吗？若一定，求∠DMF的度数；若不一定，请说明理由．

5．填空：
（1）从等式3x+5=11，得到3x=11-5的依据是等式的基本性质1；
（2）从5x=2x+3，得到5x-2x=3的依据是等式的基本性质1；
（3）从$\frac{1}{3}$x=2，得到x=2×3的依据是等式的基本性质2；
（4）从-3x=6，得到x=-2的依据是等式的基本性质3．

15．

如图，△ABC顶点A、B、C都在⊙O上，连接AO、BO，若∠OAB=50°，则∠ACB的大小是（　　）

16．已知x-y=5xy，求$\frac{2x+3xy-2y}{x-2xy-y}$的值．

试题分类