Question

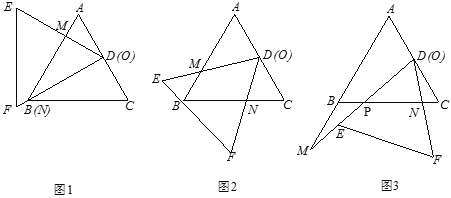
【题目】如图，正方形两条对角线、交于，过任作一直线与边，交于，，的垂直平分线与边，交于，．设正方形的面积为，四边形的面积为．

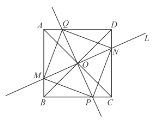
（1）求证：四边形是正方形；

（2）若，求的取值范围．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

(1)先根据正方形的性质和垂直平分线的定义证明≌，可得,再根据等边对等角证明，同理可证，由此可证四边形是矩形，而又，所以可证矩形是正方形．

(2)设，则，根据勾股定理表示，即可表示，再根据函数最值结合图形，即可确定的取值范围．

解：（1）证明：∵四边形为正方形，

∴AC⊥BD，∠OAQ=∠ODN=45°，OA=OD，

∴∠AOQ+∠DOQ=90°，

∵垂直平分线段，

∴∠QON=90°，，

∴∠DON+∠DOQ=90°,

∴∠DON=∠AOQ，

在△AOQ和△DON中，

∵

∴≌，

∴，

∴，

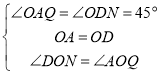
同理可得，

∴，

∴四边形是矩形，而，

∴四边形是正方形．

（2）∵≌，

∴AQ=DN，

设，则，

∴

而，

∴．