Question

4．如图，已知点A（6，0），O为坐标原点，P是线段OA上任意一点（不含端点O，A），过P，O两点的二次函数y₁和过P，A两点的二次函数y₂的图象开口均向下，它们的顶点分别为B，C，射线OB与射线AC相交于点D，当△ODA是等边三角形时，这两个二次函数的最大值之和等于（　　）

• A． $\sqrt{5}$
• B． $\frac{4}{3}$$\sqrt{5}$
• C． 3$\sqrt{3}$
• D． $\frac{3}{2}$$\sqrt{3}$

Answer 1

分析 连接PB、PC，根据二次函数的对称性可知OB=PB，PC=AC，从而判断出△POB和△ACP是等边三角形，再根据等边三角形的性质求解即可．

解答 解：如图，连接PB、PC，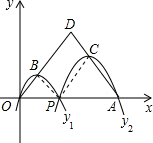
由二次函数的性质，OB=PB，PC=AC，
∵△ODA是等边三角形，
∴∠AOD=∠OAD=60°，
∴△POB和△ACP是等边三角形，
∵A（6，0），
∴OA=6，
∴点B、C的纵坐标之和为6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$，
即两个二次函数的最大值之和等于3$\sqrt{3}$．
故选：C．

点评 本题考查了二次函数的最值问题，等边三角形的判定与性质，作辅助线构造出等边三角形并利用等边三角形的知识求解是解题的关键．