题目内容
20.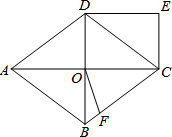 如图,菱形ABCD中,对角线AC,BD交于O点,DE∥AC,CE∥BD.
如图,菱形ABCD中,对角线AC,BD交于O点,DE∥AC,CE∥BD.(1)求证:四边形OCED为矩形;
(2)在BC截取CF=CO,连接OF,若AC=8,BD=6,求四边形OFCD的面积.
分析 (1)根据对边得出是平行四边形,再根据AC⊥BD证明出四边形OCED为矩形;
(2)根据菱形的性质和直角三角形中的三角函数进行计算,问题得解.
解答 (1)证明:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形.
又∵四边形ABCD是菱形,
∴AC⊥BD.
∴∠DOC=90°.
∴四边形OCED为矩形.
(2)∵四边形ABCD是菱形,
∴AC与BD互相垂直平分于点O,
∴OD=OB=$\frac{1}{2}$BD=3,OA=OC=$\frac{1}{2}$AC=4,
∴S△DOC=$\frac{1}{2}OD•OC$=$\frac{1}{2}×3×4$=6.
在Rt△OBC中,
BC=$\sqrt{O{B^2}+O{C^2}}$=5,sin∠OCB=$\frac{OB}{BC}$=$\frac{3}{5}$.
作FH⊥OC于点H,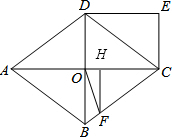
在Rt△CFH中,CF=CO=4,sin∠HCF=$\frac{FH}{FC}$=$\frac{3}{5}$,
∴FH=$\frac{3}{5}$CF=$\frac{12}{5}$.
∴S△OCF=$\frac{1}{2}OC•FH$=$\frac{1}{2}×4×\frac{12}{5}$=$\frac{24}{5}$.
∴S四边形OFCD=S△DOC+S△OCF=6+$\frac{24}{5}$=$\frac{54}{5}$.
点评 此题考查了菱形的判定与性质以及三角函数.此题难度不大,注意证得四边形CODE是矩形是解此题的关键.

练习册系列答案
相关题目
5.下列代数式中是二次二项式的是( )
| A. | xy-1 | B. | $\frac{1}{{x}^{2}+1}$ | C. | x2+xy2 | D. | $\sqrt{{x}^{4}+1}$ |
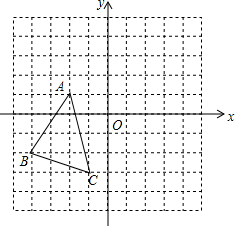 如图,在平面直角坐标系中,△ABC的顶点都在网格点上,将△ABC先向右平移5个单位长度,再向上平移2个单位长度,得到△A′B′C′.
如图,在平面直角坐标系中,△ABC的顶点都在网格点上,将△ABC先向右平移5个单位长度,再向上平移2个单位长度,得到△A′B′C′. 如图,菱形ABCD的边长为5cm,对角线BD的长为6cm,则菱形ABCD的面积为24cm2.
如图,菱形ABCD的边长为5cm,对角线BD的长为6cm,则菱形ABCD的面积为24cm2.