题目内容
14. 如图,已知点A是双曲线y=$\frac{2\sqrt{6}}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-6$\sqrt{6}$.
如图,已知点A是双曲线y=$\frac{2\sqrt{6}}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-6$\sqrt{6}$.
分析 设点A的坐标为(a,$\frac{2\sqrt{6}}{a}$),连接OC,则OC⊥AB,表示出OC,过点C作CD⊥x轴于点D,设点C的坐标为(x,y),在Rt△OCD中,在Rt△COD中利用勾股定理可得出x2的值,进而得出结论.
解答 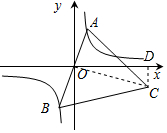 解:如图,设A(a,$\frac{2\sqrt{6}}{a}$).
解:如图,设A(a,$\frac{2\sqrt{6}}{a}$).
∵点A与点B关于原点对称,
∴OA=OB.
∵△ABC为等边三角形,
∴AB⊥OC,OC=$\sqrt{3}$AO,
∵AO=$\sqrt{{a}^{2}+\frac{24}{{a}^{2}}}$,
∴CO=$\sqrt{3{a}^{2}+\frac{72}{{a}^{2}}}$,
过点C作CD⊥x轴于点D,设点C的坐标为(x,y),
∵∠AOD=∠OCD=90°-∠COD,
∴tan∠AOD=tan∠OCD,即$\frac{\frac{2\sqrt{6}}{a}}{a}$=$\frac{x}{-y}$,
解得y=-$\frac{{a}^{2}}{2\sqrt{6}}$x.
在Rt△COD中,CD2+OD2=OC2,即y2+x2=3a2+$\frac{72}{{a}^{2}}$,
将y=-$\frac{{a}^{2}}{2\sqrt{6}}$x代入,可得:x2=$\frac{72}{{a}^{2}}$,
故x=$\frac{6\sqrt{2}}{a}$,y=-$\frac{{a}^{2}}{2\sqrt{6}}$x=-$\sqrt{3}$a,
则xy=-6$\sqrt{6}$,即k=-6$\sqrt{6}$.
故答案为:-6$\sqrt{6}$.
点评 本题考查的是反比例函数图象上点的坐标特点,等腰三角形的性质,反比例函数的性质,勾股定理,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

 如图是婴儿车的平面示意图,其中AB∥CD,∠1=124°,∠3=40°,那么∠2的度数为( )
如图是婴儿车的平面示意图,其中AB∥CD,∠1=124°,∠3=40°,那么∠2的度数为( )| A. | 74° | B. | 76° | C. | 84° | D. | 86° |
| A. | $\frac{84}{83}$和$\frac{88}{87}$ | B. | $\frac{86}{85}$和$\frac{88}{87}$ | C. | $\frac{85}{84}$和$\frac{87}{86}$ | D. | $\frac{86}{85}$和$\frac{87}{86}$ |
| A. | 1 | B. | 3 | C. | $\sqrt{3}$ | D. | 4 |
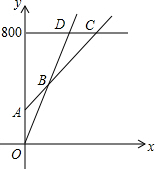 某市游泳馆为了满足不同顾客的需求,设计了三种游泳票:普通票价每次20元/张;金卡售价800元/张,每次凭卡不再收费;银卡售价200元/张,每次凭卡另收10元.这样顾客可根据游泳次数的多少选择不同的消费方式.普通票全年正常出售,两种优惠卡仅限暑期使用,不限次数.设游泳x次时,所需总费用为y元.
某市游泳馆为了满足不同顾客的需求,设计了三种游泳票:普通票价每次20元/张;金卡售价800元/张,每次凭卡不再收费;银卡售价200元/张,每次凭卡另收10元.这样顾客可根据游泳次数的多少选择不同的消费方式.普通票全年正常出售,两种优惠卡仅限暑期使用,不限次数.设游泳x次时,所需总费用为y元.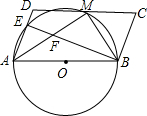 在?ABCD中,以AB为直径的⊙O交CD于M,交AD于E,且AM平分∠BAD,连接BE交AM于F,若AD=5,AM=8,则MF的长为$\frac{9}{2}$.
在?ABCD中,以AB为直径的⊙O交CD于M,交AD于E,且AM平分∠BAD,连接BE交AM于F,若AD=5,AM=8,则MF的长为$\frac{9}{2}$.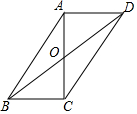 如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,若$\frac{BD}{CD}$=$\frac{8}{5}$,则$\frac{BC}{AC}$=$\frac{\sqrt{39}}{6}$.
如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,若$\frac{BD}{CD}$=$\frac{8}{5}$,则$\frac{BC}{AC}$=$\frac{\sqrt{39}}{6}$.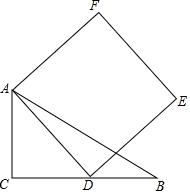 如图.己知△ABC中.∠C=90°,AC=3,BC=4.动点D在边BC上.以AD为边作正方形ADEF.在点D从点C移动至点B的过程中.点E移动的路线长为4$\sqrt{2}$.
如图.己知△ABC中.∠C=90°,AC=3,BC=4.动点D在边BC上.以AD为边作正方形ADEF.在点D从点C移动至点B的过程中.点E移动的路线长为4$\sqrt{2}$.