题目内容
13.计算:(1)(2x+3y)2-(4x-9y)(4x+9y)+(3x-2y)2.
(2)(a-2b)2-(2a+b)(b-2a)-4a(a-b)
分析 (1)、(2)先算乘方,乘法,再合并同类项即可.
解答 解:(1)原式=4x2+9y2+12xy-16x2+81y2+9x2+4y2-12xy
=-3x2+94y2;
(2)原式=a2-4ab+4b2-b2+4a2-4a2+4ab
=a2+3b2.
点评 本题考查的是平方差公式、完全平方公式、单项式乘以多项式及合并同类项得相关知识,熟记完全平方公式是解答此题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
3.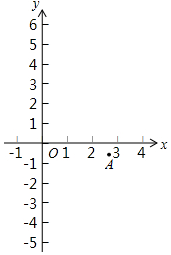 有这样一个问题:探究函数y=(x-1)(x-2)(x-3)的图象与性质.小东对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究.
有这样一个问题:探究函数y=(x-1)(x-2)(x-3)的图象与性质.小东对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
(1)函数y=(x-1)(x-2)(x-3)的自变量x的取值范围是全体实数;
(2)下表是y与x的几组对应值.
①m=-60;
②若M(-7,-720),N(n,720)为该函数图象上的两点,则n=11;
(3)在平面直角坐标系xOy中,A(xA,yA),B(xB,-yA)为该函数图象上的两点,且A为2≤x≤3范围内的最低点,A点的位置如图所示.
①标出点B的位置;
②画出函数y=(x-1)(x-2)(x-3)(0≤x≤4)的图象.
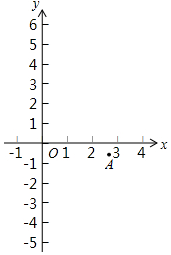 有这样一个问题:探究函数y=(x-1)(x-2)(x-3)的图象与性质.小东对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究.
有这样一个问题:探究函数y=(x-1)(x-2)(x-3)的图象与性质.小东对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究.下面是小东的探究过程,请补充完成:
(1)函数y=(x-1)(x-2)(x-3)的自变量x的取值范围是全体实数;
(2)下表是y与x的几组对应值.
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| y | … | m | -24 | -6 | 0 | 0 | 0 | 6 | 24 | 60 | … |
②若M(-7,-720),N(n,720)为该函数图象上的两点,则n=11;
(3)在平面直角坐标系xOy中,A(xA,yA),B(xB,-yA)为该函数图象上的两点,且A为2≤x≤3范围内的最低点,A点的位置如图所示.
①标出点B的位置;
②画出函数y=(x-1)(x-2)(x-3)(0≤x≤4)的图象.
5.小明所在的九年级一班共有38名学生,一次体检测量了全班学生的身高,由此求得该班学生的平均身高是1.67米,而小明的身高是1.66米,则下列说法错误的是( )
| A. | 1.67米是该班学生身高的平均水平 | |
| B. | 班上比小明矮的学生人数不会超过19人 | |
| C. | 这组身高数据的中位数不一定是1.67米 | |
| D. | 这组身高数据的众数不一定是1.67米 |
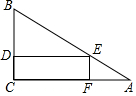 一块三角形材料如图所示,∠A=30°,∠C=90°,AB=12,用这块材料剪出一个矩形CDEF,其中D、E、F分别在BC、AB、AC上.
一块三角形材料如图所示,∠A=30°,∠C=90°,AB=12,用这块材料剪出一个矩形CDEF,其中D、E、F分别在BC、AB、AC上.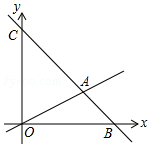 如图,在平面直角坐标系中,直线AB交x轴于点B(6,0),交y轴于点C(0,6),直线AB与直线OA:y=$\frac{1}{2}$x相交于点A,动点M在线段OA和射线AC上运动.
如图,在平面直角坐标系中,直线AB交x轴于点B(6,0),交y轴于点C(0,6),直线AB与直线OA:y=$\frac{1}{2}$x相交于点A,动点M在线段OA和射线AC上运动.