题目内容
3.在平面直角坐标系中,A(2,0),B(-2,0),C(0,-3),求点D坐标,使A、B、C、D四点组成平行四边形,并求出对应面积.分析 直接利用平行四边形的性质结合其面积求法得出符合题意的答案.
解答  解:如图所示:D1(0,3),D2(-4,-3),D3(4,-3),
解:如图所示:D1(0,3),D2(-4,-3),D3(4,-3),
四边形ABCD1的面积为:$\frac{1}{2}$×4×6=12;
四边形ABCD2的面积=四边形ABCD3的面积为:3×4=12.
点评 此题主要考查了平行四边形的判定以及平行四边形的面积,正确得出D点位置是解题关键.

练习册系列答案
相关题目
11. 如图,在矩形ABCD中,点O为对角线AC、BD的交点,点E为BC上一点,连接EO,并延长交AD于点F,则图中全等三角形共有( )
如图,在矩形ABCD中,点O为对角线AC、BD的交点,点E为BC上一点,连接EO,并延长交AD于点F,则图中全等三角形共有( )
 如图,在矩形ABCD中,点O为对角线AC、BD的交点,点E为BC上一点,连接EO,并延长交AD于点F,则图中全等三角形共有( )
如图,在矩形ABCD中,点O为对角线AC、BD的交点,点E为BC上一点,连接EO,并延长交AD于点F,则图中全等三角形共有( )| A. | 5对 | B. | 6对 | C. | 8对 | D. | 10对 |
13. 某校组织全校2 000名学生进行了环保知识竞赛.为了解成绩的分布情况,随机抽取了部分学生的成绩(得分取整数,满分为100分),并绘制了频数分布表和频数分布直方图(不完整):
某校组织全校2 000名学生进行了环保知识竞赛.为了解成绩的分布情况,随机抽取了部分学生的成绩(得分取整数,满分为100分),并绘制了频数分布表和频数分布直方图(不完整):
根据所给信息,回答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)学校将对成绩在90.5~100.5分之间的学生进行奖励,请你估算出全校获奖学生的人数.
 某校组织全校2 000名学生进行了环保知识竞赛.为了解成绩的分布情况,随机抽取了部分学生的成绩(得分取整数,满分为100分),并绘制了频数分布表和频数分布直方图(不完整):
某校组织全校2 000名学生进行了环保知识竞赛.为了解成绩的分布情况,随机抽取了部分学生的成绩(得分取整数,满分为100分),并绘制了频数分布表和频数分布直方图(不完整):| 分组 | 频数 | 频率 |
| 50.5~60.5 | 20 | 0.05 |
| 60.5~70.5 | 48 | △ |
| 70.5~80.5 | △ | 0.20 |
| 80.5~90.5 | 104 | 0.26 |
| 90.5~100.5 | 148 | △ |
| 合计 | △ | 1 |
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)学校将对成绩在90.5~100.5分之间的学生进行奖励,请你估算出全校获奖学生的人数.
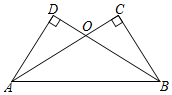 已知:AC⊥BC,BD⊥AD,AC 与BD 交于O,AC=BD,∠CAB=32°.求∠DAB的度数.
已知:AC⊥BC,BD⊥AD,AC 与BD 交于O,AC=BD,∠CAB=32°.求∠DAB的度数.