题目内容

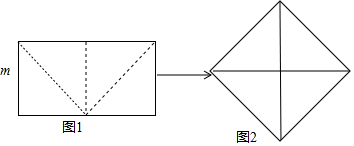
12．如图，在Rt△ABC中，AB=18，BC=12，将△ABC折叠，使A点与BC的中点D重合，折痕为EF，则线段DF的长为10．

分析 设FB=x，则AF=18-x，由翻折的性质可知FD=AF=18-x，然后在△BFD中利用勾股定理列方程求解即可．

解答 解：设FB=x，则AF=18-x．
由翻折的性质可知：FD=AF=18-x．
∵点D是BC的中点，
∴BD=$\frac{1}{2}$BC=6．
在Rt△FBD中，由勾股定理可知：FD2=FB2+DB2，即（18-x）2=x2+62，
解得：x=8．
∴DF=18-x=10．
故答案为10．

点评 本题主要考查的是翻折的性质和勾股定理的应用，利用翻折的性质得到FD=AF=18-x是解题的关键．

练习册系列答案
相关题目
2．如图，线段AC、BD交于点M，过B、D两点分别作AC的垂线段BF、DE，AB=CD
（1）若∠A=∠C，求证：FM=EM；
（2）若FM=EM，则∠A=∠C．是真命题吗？（直接判断，不必证明）
3．如图△ABC的三个顶点在网格中格点上，求sinA=$\frac{3}{5}$．
20．已知矩形OABC在如图所示平面直角坐标系中，点B的坐标为（4，3），连接AC．动点P从点B出发，以2cm/s的速度，沿直线BC方向运动，运动到C为止（不包含B、C两点），过点P作PQ∥AC交线段BA于点Q，以PQ为边向下作正方形PQMN，设正方形PQMN与△ABC重叠部分图形面积为S（cm2），设点P的运动时间为t（s）．
（1）请用含t的代数式表示N点的坐标；
（2）求S与t之间的函数关系式，并指出t的取值范围；
（3）如图②，点G在边OC上，且OG=1cm，在点P从点B出发的同时，另有一动点E从点O出发，以2cm/s的速度，沿x轴正方向运动，以OG、OE为一组邻边作矩形OEFG．请直接写出当点F落在正方形PQMN的内部（不含边界）时t的取值范围．
7．在Rt△ABC中，∠ACB=90°，AC=BC=2，点P为边BC上的一动点（不与B、C重合），点P关于直线AC、AB的对称点分别为M、N，连接MN交边AB于点F，交边AC于点E．
（1）如图1，当点P为边BC的中点时，求∠M的正切值；
（2）连接FP，设CP=x，S△MPF=y，求y关于x的函数关系式，并写出定义域；
（3）连接AM，当点P在边BC上运动时，△AEF与△ABM是否一定相似？若是，请证明；若不是，请求出当△AEF与△ABM相似时CP的长．
17．已知y1=a1（x-m）2+5，点（m，25）在抛物线y2=a2x2+b2x+c2上，其中m＞0．
（1）若a1=-1，点（1，4）在抛物线y1=a1（x-m）2+5上，求m的值；
（2）记O为坐标原点，抛物线y2=a2x2+b2x+c2的顶点为M，若c2=0，点A（2，0）在此抛物线上，∠OMA=90°，求点M的坐标；
（3）若y1+y2=x2+16x+13，且4a2c2-b22=-8a2，求抛物线y2=a2x2+b2x+c2的解析式．
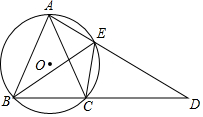4．如图，△ABC内接于⊙O，且AB=AC，延长BC至点D，使CD=AC，连接AD交⊙O交于点E，连接BE，CE．
（1）求证：AE=CE；
（2）若CE∥AB，求证：DE2=AE•AD．
1．如图1，将宽为m，长是宽的2倍的长方形沿虚线剪开，得到四个直角三角形，这四个直角三角形可以拼成一个如图2的大正方形．
（1）图1中的长方形的面积和图2中的正方形的面积的关系是：相等；
（2）当m=2和m=3时，分别求图2中大正方形的边长；
（3）通过（2）问猜想图2中的大正方形的边长n与图1中长方形的宽m有何关系，并证明你的猜想．
2．已知∠1与∠2互余，∠2与∠3互补，∠1=67°12′，则∠3=157°12′．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网