题目内容
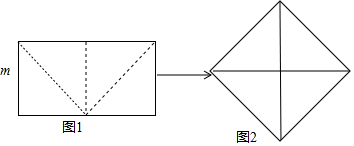
1.如图1,将宽为m,长是宽的2倍的长方形沿虚线剪开,得到四个直角三角形,这四个直角三角形可以拼成一个如图2的大正方形.(1)图1中的长方形的面积和图2中的正方形的面积的关系是:相等;
(2)当m=2和m=3时,分别求图2中大正方形的边长;
(3)通过(2)问猜想图2中的大正方形的边长n与图1中长方形的宽m有何关系,并证明你的猜想.
分析 (1)先求出长方形的面积,由剪开和拼图知,图2中大正方形的边长为$\sqrt{2}$m,即可得出正方形的面积即可;
(2)利用(1)的结论直接代值即可;
(3)同(1)的方法得出结论.
解答 解:(1)如图, 由题意知,AB=CD=m,AD=BC=2m,
由题意知,AB=CD=m,AD=BC=2m,
∴S长方形ABCD=AB×BC=m×2m=2m2;
∵宽为m,长是宽的2倍的长方形沿虚线剪开,得到四个直角三角形,
此四个直角三角形全等的等腰直角三角形,
∴斜边是长方形的宽的$\sqrt{2}$倍;
∴AN=DN=$\sqrt{2}$m,
拼成如图2所示的四边形,此四边形是正方形,边长为$\sqrt{2}$m;
∴EO=FO=GO=HO=$\sqrt{2}$m,
∴EG=FH=2$\sqrt{2}$m,
∴S正方形EFGH=$\frac{1}{2}$EG×FH=$\frac{1}{2}$×$\sqrt{2}$m×$\sqrt{2}$m=2m2,
∴S长方形ABCD=S正方形EFGH,
故答案为:相等;
(2)由(1)知,图2中大正方形的边长为EF=$\sqrt{2}$m,
当m=2时,图2中大正方形的边长为EF=$\sqrt{2}$m=2$\sqrt{2}$,
当m=3时,图2中大正方形的边长为EF=$\sqrt{2}$m=3$\sqrt{2}$,
(3)n=$\sqrt{2}$m,
理由:∵宽为m,长是宽的2倍的长方形沿虚线剪开,得到四个直角三角形,
此四个直角三角形全等的等腰直角三角形,
∴斜边是长方形的宽的$\sqrt{2}$倍;
图2中是以图1剪开的四个全等的等腰直角三角形的斜边为边.
∴n=$\sqrt{2}$m,
点评 此题是四边形综合题,主要考查了长方形的性质,正方形的性质和面积公式,勾股定理,剪图和拼图问题,解本题的关键是图1中的量到图2中的量之间的关系.

 备战中考寒假系列答案
备战中考寒假系列答案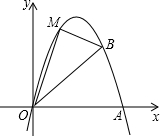 如图,在平面直角坐标系中,己知点A(5,0),B(4,4)
如图,在平面直角坐标系中,己知点A(5,0),B(4,4) 如图,在Rt△ABC中,AB=18,BC=12,将△ABC折叠,使A点与BC的中点D重合,折痕为EF,则线段DF的长为10.
如图,在Rt△ABC中,AB=18,BC=12,将△ABC折叠,使A点与BC的中点D重合,折痕为EF,则线段DF的长为10. 如图,圆中的弦AB与弦CD垂直于点E,点F在$\widehat{BC}$上,$\widehat{AC}$=$\widehat{BF}$,直线MN过点D,且∠MDC=∠DFC,求证:直线MN是该圆的切线.
如图,圆中的弦AB与弦CD垂直于点E,点F在$\widehat{BC}$上,$\widehat{AC}$=$\widehat{BF}$,直线MN过点D,且∠MDC=∠DFC,求证:直线MN是该圆的切线.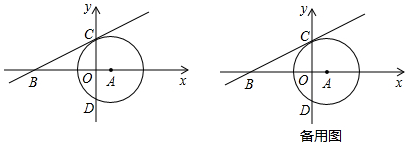
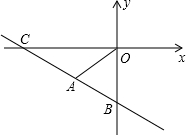 如图,一次函数y=ax-b与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于B(0,-4),且OA=AB,△AOB的面积为6.
如图,一次函数y=ax-b与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于B(0,-4),且OA=AB,△AOB的面积为6. 如图,等腰三角形ABC中,AB=AC=5cm,BC=6cm,动点P从点A出发,沿路线A-B-C匀速运动,速度为1cm/s,运动到C点停止,设运动时间为t(s),△APC的面积为y(cm2).
如图,等腰三角形ABC中,AB=AC=5cm,BC=6cm,动点P从点A出发,沿路线A-B-C匀速运动,速度为1cm/s,运动到C点停止,设运动时间为t(s),△APC的面积为y(cm2).