题目内容
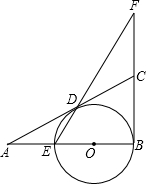 如图,在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB长为半径的圆与AB交于点E,与AC相切于点D,直线ED交BC的延长线于点F.
如图,在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB长为半径的圆与AB交于点E,与AC相切于点D,直线ED交BC的延长线于点F.(1)求证:BC=FC;
(2)若AD:AE=2:1,求tan∠F的值.
考点:切线的性质
专题:
分析:(1)首先连接BD,由等角的余角相等,易证得∠F=∠EBD.由弦切角定理,易证得∠F=∠CDF.可得CD=CF,又由切线长定理,可得CD=CB,继而可证得BC=FC;
(2)易证得△ADE∽△ABD,然后由相似三角形的对应边成比例,可求得DE:BD=1:2,又由∠F=∠EBD.可求得tan∠F=tan∠EBD=
=
.
(2)易证得△ADE∽△ABD,然后由相似三角形的对应边成比例,可求得DE:BD=1:2,又由∠F=∠EBD.可求得tan∠F=tan∠EBD=
| DE |
| BD |
| 1 |
| 2 |
解答: (1)证明:连接BD.
(1)证明:连接BD.
∵BE是直径,
∴∠BDE=90°,
∴∠EBD=90°-∠BED.
∵∠EBF=90°,
∴∠F=90°-∠BEF.
∴∠F=∠EBD.
∵⊙O切AC于D,
∴∠EBD=∠ADE=∠CDF.
∴∠F=∠CDF.
∴CD=CF,
∵OB⊥BC,
∴BC是⊙O的切线,
由切线长定理可知:CD=CB.
∴BC=FC.
(2)解:在△ADE和△ABD中,
∵∠A=∠A,∠ADE=∠ABD,
∴△ADE∽△ABD,
∴
=
,
∵AD:AE=2:1.
∴DE:BD=1:2,
又∵∠F=∠EBD.
∴tan∠F=tan∠EBD=
=
.
 (1)证明:连接BD.
(1)证明:连接BD.∵BE是直径,
∴∠BDE=90°,
∴∠EBD=90°-∠BED.
∵∠EBF=90°,
∴∠F=90°-∠BEF.
∴∠F=∠EBD.
∵⊙O切AC于D,
∴∠EBD=∠ADE=∠CDF.
∴∠F=∠CDF.
∴CD=CF,
∵OB⊥BC,
∴BC是⊙O的切线,
由切线长定理可知:CD=CB.
∴BC=FC.
(2)解:在△ADE和△ABD中,
∵∠A=∠A,∠ADE=∠ABD,
∴△ADE∽△ABD,
∴
| AE |
| AD |
| DE |
| BD |
∵AD:AE=2:1.
∴DE:BD=1:2,
又∵∠F=∠EBD.
∴tan∠F=tan∠EBD=
| DE |
| BD |
| 1 |
| 2 |
点评:此题考查了切线的性质、相似三角形的判定与性质、弦切角定理、切线长定理以及等腰三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
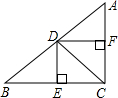 如图,在Rt△ABC中,∠ACB=90°,CD平分∠ACB,过点D分别作DE⊥BC,DF⊥AC,垂足分别为E,F.
如图,在Rt△ABC中,∠ACB=90°,CD平分∠ACB,过点D分别作DE⊥BC,DF⊥AC,垂足分别为E,F.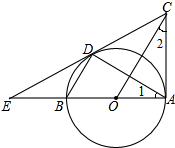 已知A、D为⊙O的切点,AB为直径,延长AB交D所在的切线于点E,A所在的切线交于点C.求证:
已知A、D为⊙O的切点,AB为直径,延长AB交D所在的切线于点E,A所在的切线交于点C.求证: 如图,D、E分别为等边△ABC的边BC、AC上一点,BD=CE,∠CAD=45°,AD、BE交于M.
如图,D、E分别为等边△ABC的边BC、AC上一点,BD=CE,∠CAD=45°,AD、BE交于M.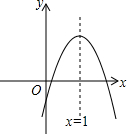 已知:二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①b>0;②c<0;③4a+2b+c>0;④(a+c)2<b2,正确的是
已知:二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①b>0;②c<0;③4a+2b+c>0;④(a+c)2<b2,正确的是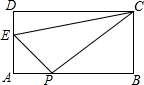 如图,在矩形ABCD中,AB=7,BC=3,E在AD上,且AE=2,在边AB是否存在点P,使得以P、A、E为顶点的三角形与以P、B、C为顶点的三角形相似?若不存在,请说明理由;若存在,这样的点有几个?并计算出AP的长.
如图,在矩形ABCD中,AB=7,BC=3,E在AD上,且AE=2,在边AB是否存在点P,使得以P、A、E为顶点的三角形与以P、B、C为顶点的三角形相似?若不存在,请说明理由;若存在,这样的点有几个?并计算出AP的长.