Question

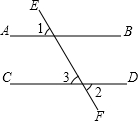填空：已知：如图，∠1=∠2，求证：AB∥CD
证明：∵∠1=∠2，（已知）
又∠3=∠2，

 

∴∠1=

 

．

 

∴AB∥CD．

 

．

Answer 1

考点：平行线的判定

专题：推理填空题

分析：根据对顶角相等和等量代换可以推知同位角∠1=∠3，则由“同位角相等，两直线平行”可以判定AB∥CD

解答：证明：∵∠1=∠2，（已知）
又∠3=∠2，（对顶角相等）
∴∠1=∠3． （等量代换）
∴AB∥CD． （同位角相等，两直线平行）．
故答案是：（对顶角相等）；∠3；（等量代换）；（同位角相等，两直线平行）．

点评：本题考查了平行线的判定．解题时，利用了平行线的判定定理1：两条直线被第三条所截，如果同位角相等，那么这两条直线平行． 简单说成：同位角相等，两直线平行．