题目内容
5．如果抛物线y=-2x2+2mx-$\frac{3}{4}$的顶点在x轴的负半轴上，求m的值．分析 由于抛物线的顶点在x轴负半轴上，那么根的判别式△=0（因为抛物线与x轴只有一个交点），且抛物线的对称轴x=-$\frac{b}{2a}$＜0；联立上述两式可求得m的值．
解答 解：∵抛物线y=-2x2+2mx-$\frac{3}{4}$的顶点在x轴的负半轴上，
∴△=（2m）2-4×（-2）×（-$\frac{3}{4}$）=0，且对称轴x=-$\frac{2m}{4}$＜0，
解得：m=±$\frac{\sqrt{6}}{2}$，且m＞0，
∴m=$\frac{\sqrt{6}}{2}$．
点评 本题主要考查了二次函数的性质，二次函数解析式的确定、二次函数与一元二次方程的关系，以及抛物线的对称轴的求法．
练习册系列答案
相关题目
15．
如图，在△ABC中，如果DE∥BC，DF∥AC，则不正确的是（ ）
如图，在△ABC中，如果DE∥BC，DF∥AC，则不正确的是（ ）| A． | $\frac{AE}{EC}$=$\frac{CF}{FB}$ | B． | $\frac{BF}{BC}$=$\frac{DF}{AC}$ | C． | $\frac{AC}{AE}$=$\frac{AB}{AC}$ | D． | $\frac{AD}{FC}$=$\frac{AB}{BC}$ |
13．方程$\frac{1}{x}$-2=x2-2x有（ ）个实数根．
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
下图是一个简单的数值运算程序，当输入x的值为-2时，则输出的数值为12．
17．有两个一元二次方程M：ax2+bx+c=0，N：cx2+bx+a=0，其中a×c≠0，a≠c；以下列四个结论中错误的是（ ）
| A． | 如果方程M有两个不相等的实数根，那么方程N也有两个不相等的实数根 | |
| B． | 如果方程M有两根符号相同，那么方程N的两根符号也相同 | |
| C． | 如果5是方程M的一个根，那么$\frac{1}{5}$是方程N的一个根 | |
| D． | 如果方程M和方程N有一个相同的根，那么这个根必是x=1 |
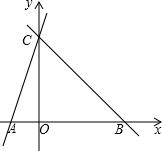如图，直线y=kx+k交x轴、y轴分别于A，C，直线BC过点C交x轴于B，OC=3OA，∠CBA=45°．