题目内容
14.已知二次函数y=ax2-4ax-3的图象与直线y=x+1相交于A、B两点,直线与y轴交于点P,A、B关于点P对称,求线段AB的长.分析 由直线y=x+1与y轴交于点P,得出P点坐标为(0,1),A、B关于点P对称,得出两个点的纵坐标之差的绝对值为2,由过B点的平行线与过A点的平行线交与点C,利用一次函数得出△ABC为等腰直角三角形解决问题.
解答 解:如图,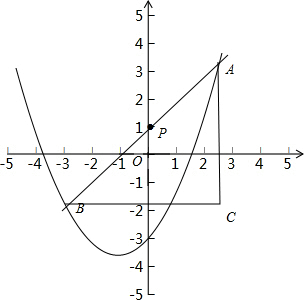
∵y=ax2-4ax-3的图象与y轴交于点(0,-3),直线y=x+1与y轴交于点P,
∴P点坐标为(0,1),
∵A、B关于点P对称,
∴AC=2,
∵y=x+1与x轴交点为(0,-1),
∴△ABC为等腰直角三角形,
∴AB=2$\sqrt{2}$.
点评 此题考查二次函数的性质,一次函数的性质,关于一点成对称点的坐标特征,求得一次函数与坐标轴的交点坐标是解决问题的关键.

练习册系列答案
相关题目
9.如果有理数a=5.93×1012,则a的整数部分的位数是( )
| A. | 13 | B. | 12 | C. | 14 | D. | 11 |
6.计算:-9+6÷(-3)的结果是( )
| A. | -11 | B. | 1 | C. | -7 | D. | -9$\frac{1}{2}$ |
9.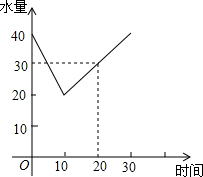 一蓄水池中有水40m3,水池里的水量与放水时间有如下关系:
一蓄水池中有水40m3,水池里的水量与放水时间有如下关系:
设放水时间为x(分钟),水池中的水量为y(m3).
(1)请直接写出y与x的关系式;
(2)当放水时间为10分钟时,求出此时水池中的水量;当水池中的水刚被放完时,经过了多少分钟?
(3)当放水10分钟后,再开放一个进水管(此时,放水与进水同时进行),则水池中的水量随着时间的变化如图所示,请根据图象求出进水管每分钟放进多少水量?
 一蓄水池中有水40m3,水池里的水量与放水时间有如下关系:
一蓄水池中有水40m3,水池里的水量与放水时间有如下关系:| 放水时间/分 | 2 | 4 | 6 | 8 | … |
| 水池中水量/m3 | 36 | 32 | 28 | 24 | … |
(1)请直接写出y与x的关系式;
(2)当放水时间为10分钟时,求出此时水池中的水量;当水池中的水刚被放完时,经过了多少分钟?
(3)当放水10分钟后,再开放一个进水管(此时,放水与进水同时进行),则水池中的水量随着时间的变化如图所示,请根据图象求出进水管每分钟放进多少水量?
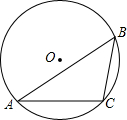 如图,⊙O是△ABC的外接圆,BC=4cm,∠A=30°,求⊙O的面积(用两种不同的方法求解).
如图,⊙O是△ABC的外接圆,BC=4cm,∠A=30°,求⊙O的面积(用两种不同的方法求解). 如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=57°,求∠CAD的度数.
如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=57°,求∠CAD的度数.