题目内容
5.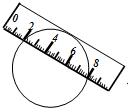 如图,两边平行的刻度尺在圆上移动,当刻度尺的一边与直径为6.5cm的圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则刻度尺的宽为2cm.
如图,两边平行的刻度尺在圆上移动,当刻度尺的一边与直径为6.5cm的圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则刻度尺的宽为2cm.
分析 根据垂径定理得BE的长,再根据勾股定理列方程求解即可.
解答 解:作OE垂直AB于E交⊙O与D,
设OB=r,
根据垂径定理,BE=$\frac{1}{2}$AB=3,
根据题意列方程得:(3.25-DE)2+9=3.252,
解得:DE=2,
∴该直尺的宽度为2cm.
故答案为:2.
点评 此题主要考查了垂径定理的应用,此题很巧妙,将垂径定理和勾股定理不露痕迹的镶嵌在实际问题中,考查了同学们的转化能力.

练习册系列答案
相关题目
15.一种球形细胞的半径约为1.1×10-6米,用小数表示是( )
| A. | 0.00000011 | B. | 0.000000011 | C. | 0.000011 | D. | 0.0000011 |
16.已知三角形两边的长分别为5cm和8cm,则第三边的长可以是( )
| A. | 3cm | B. | 9cm | C. | 14cm | D. | 18cm |
20.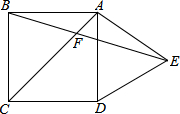 如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
 如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )| A. | 75° | B. | 60° | C. | 55° | D. | 45° |
10.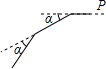 如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
 如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )| A. | 30° | B. | 40° | C. | 80° | D. | 108° |
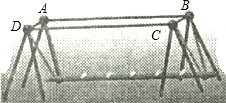 如图是一种儿童的游乐设施-儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由.
如图是一种儿童的游乐设施-儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由.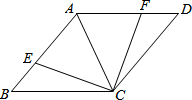 如图,AC是菱形ABCD的对角线,点E,F分别在AB,AD上,且AE=AF.求证:CE=CF.
如图,AC是菱形ABCD的对角线,点E,F分别在AB,AD上,且AE=AF.求证:CE=CF.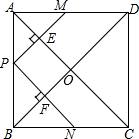 如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:
如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论: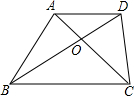 如图,梯形ABCD中,AD∥BC,AB⊥AC,AB=AC,BD=BC,若AD=$\sqrt{2}$,则梯形的面积是$\frac{5+3\sqrt{3}}{2}$.
如图,梯形ABCD中,AD∥BC,AB⊥AC,AB=AC,BD=BC,若AD=$\sqrt{2}$,则梯形的面积是$\frac{5+3\sqrt{3}}{2}$.