题目内容
20.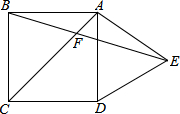 如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )| A. | 75° | B. | 60° | C. | 55° | D. | 45° |
分析 由正方形的性质和等边三角形的性质得出∠BAE=150°,AB=AE,由等腰三角形的性质和内角和得出∠ABE=∠AEB=15°,再运用三角形的外角性质即可得出结果.
解答 解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,∠BAF=45°,
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE,
∴∠BAE=90°+60°=150°,AB=AE,
∴∠ABE=∠AEB=$\frac{1}{2}$(180°-150°)=15°,
∴∠BFC=∠BAF+∠ABE=45°+15°=60°;
故选:B.
点评 本题考查了正方形的性质、等边三角形的性质、等腰三角形的判定与性质、三角形的外角性质;熟练掌握正方形和等边三角形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
15.已知△ABC∽△DEF,且相似比为2:3,则△ABC与△DEF的对应高之比为( )
| A. | 2:3 | B. | 3:2 | C. | 4:9 | D. | 9:4 |
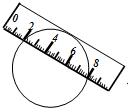 如图,两边平行的刻度尺在圆上移动,当刻度尺的一边与直径为6.5cm的圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则刻度尺的宽为2cm.
如图,两边平行的刻度尺在圆上移动,当刻度尺的一边与直径为6.5cm的圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则刻度尺的宽为2cm. 已知:如图,在△ABC中,点D在边BC上,AB=AC,∠DAE=∠BAC,AE=AD,联结DE、BE.
已知:如图,在△ABC中,点D在边BC上,AB=AC,∠DAE=∠BAC,AE=AD,联结DE、BE.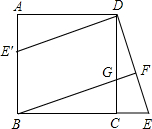 如图,在正方形ABCD中,G是CD上一点,延长BC到点E,CE=CG,连接BG并延长交DE于F.
如图,在正方形ABCD中,G是CD上一点,延长BC到点E,CE=CG,连接BG并延长交DE于F.