Question

3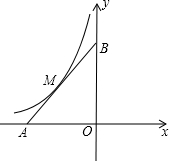．已知，在平面直角坐标系xOy中，点A在x轴负半轴上，点B在y轴正半轴上，OA=OB，函数y=-$\frac{9}{x}$的图象与线段AB交于M点，且AM=BM．
（1）求点M的坐标；
（2）求直线AB的解析式．

Answer 1

分析 （1）过点M作MC⊥x轴，MD⊥y轴，根据AM=BM可得M到x轴和y轴的距离相等，则横纵坐标互为相反数，设点M的坐标可以表示为（-a，a），代入反比例函数解析式求得a的值，得到M的坐标；
（2）根据M是AB的中点，则MC和MD是△AOB的中位线，求得OA和OB的长，即求得A和B的坐标，利用待定系数法求得AB的解析式．

解答 解：（1）过点M作MC⊥x轴，MD⊥y轴，
∵AM=BM，∴点M为AB的中点，
∵MC⊥x轴，MD⊥y轴，
∴MC∥OB，MD∥OA，
∴点C和点D分别为OA与OB的中点，
∴MC=MD，
则点M的坐标可以表示为（-a，a），
把M（-a，a）代入函数y=-$\frac{9}{x}$中，
解得a=3，
则点M的坐标为（-3，3）；

（2）∵点M的坐标为（-3，3），
∴MC=3，MD=3，
∴OA=OB=2MC=6，
∴A（-6，0），B（0，6），
设直线AB的解析式为y=kx+b，
把点A（-6，0）和B（0，6）分别代入y=kx+b中得$\left\{\begin{array}{l}{-6k+b=0}\\{b=6}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=1}\\{b=6}\end{array}\right.$，则直线AB的解析式为y=x+6．

点评 此题考查了反比例函数与一次函数的交点问题，平行线分线段成比例定理，以及中位线定理，用待定系数法确定函数的解析式，是常用的一种解题方法．同学们要熟练掌握这种方法．