题目内容
18.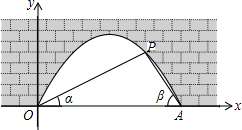 图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=$\frac{1}{2}$,tanβ=$\frac{3}{2}$,以O为原点,OA所在直线为x轴建立直角坐标系.
图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=$\frac{1}{2}$,tanβ=$\frac{3}{2}$,以O为原点,OA所在直线为x轴建立直角坐标系.(1)求点P的坐标;
(2)水面上升1m,水面宽多少?
分析 (1)过点P作PH⊥x轴于点H,设PH=3x,则OH=6x,AH=2x,由OA=4m,可求出x值,进而可得出点P的坐标;
(2)根据点O、P、A的坐标利用待定系数法,可求出抛物线的解析式,再根据二次函数图象上点的坐标特征可求出y=1时x的值,两值做差即可得出结论.
解答 解:(1)过点P作PH⊥x轴于点H,如图所示.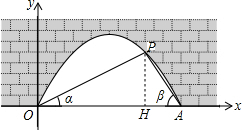
设PH=3x,则OH=6x,AH=2x,
∴OA=OH+HA=6x+2x=4,
解得:x=$\frac{1}{2}$,
∴OH=6x=3,PH=3x=$\frac{3}{2}$,
∴点P的坐标为(3,$\frac{3}{2}$).
(2)设拱桥所在抛物线的解析式为y=ax2+bx+c,
将点O(0,0)、B(4,0)、P(3,$\frac{3}{2}$)代入y=ax2+bx+c,
$\left\{\begin{array}{l}{c=0}\\{16a+4b+c=0}\\{9a+3b+c=\frac{3}{2}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=2}\\{c=0}\end{array}\right.$,
∴拱桥所在抛物线的解析式为y=-$\frac{1}{2}$x2+2x.
当y=-$\frac{1}{2}$x2+2x=1时,x=2±$\sqrt{2}$,
∴2+$\sqrt{2}$-(2-$\sqrt{2}$)=2$\sqrt{2}$(m).
答:水面上升1m,水面宽2$\sqrt{2}$m
点评 本题考查了解直角三角形的应用中的仰角俯角问题、二次函数的应用、待定系数法求二次函数解析式以及二次函数图象上点的坐标特征,解题的关键是:(1)设出PH的长度,用其表示出OH、AH的长度;(2)根据点的坐标利用待定系数法求出二次函数的解析式.


| A. | 80 | B. | 89 | C. | 99 | D. | 109 |
 如图,已知A点坐标为(5,0),直线y=kx+b(b>0)与y轴交于点B,∠BCA=60°,连接AB,∠α=105°,则直线y=kx+b的表达式为( )
如图,已知A点坐标为(5,0),直线y=kx+b(b>0)与y轴交于点B,∠BCA=60°,连接AB,∠α=105°,则直线y=kx+b的表达式为( )| A. | $y=\frac{{\sqrt{3}}}{5}x+5$ | B. | $y=\sqrt{3}x+5$ | C. | $y=\sqrt{3}x-5$ | D. | $y=-\frac{{\sqrt{3}}}{3}x+5$ |
| A. |  | B. |  | C. |  | D. |  |
| A. | (x+2)(x-2)=x2-4 | B. | x2-2x+1=(x-1)2 | C. | a2-2a+2=(a-1)2+1 | D. | 4a2-8a=2a(2a-4) |
