题目内容
7.如图,⊙O是△ABC的外接圆,∠A=30°,AB是⊙O的直径,过点C作⊙O的切线,交AB延长线于D,CD=6$\sqrt{3}$cm.
(1)求证:AC=CD;
(2)求AB的长;
(3)若动点M以3cm/s的速度从A出发沿AB方向运动,同时点N以1.5cm/s的速度从B点出发沿BC方向运动,设运动的时间为t(0≤t≤2),连接△BMN,当t为何值时△BMN为直角三角形?
分析 (1)连接OC,根据等腰三角形的性质得到∠OCA=∠A=30°,根据切线的性质得到∠OCD=90°,计算出∠D=30°,根据等腰三角形的判定定理证明即可;
(2)根据正切的概念求出OC的长,计算出AB的长;
(3)分∠MNB=90°和∠NMB=90°两种情况,根据相似三角形的判定定理和性质定理列出比例式,计算即可.
解答 (1)证明: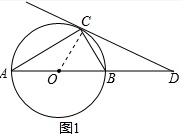 如图1,连接OC,
如图1,连接OC,
∵OA=OC,
∴∠OCA=∠A=30°,
∴∠COD=60°,
∵CD为⊙O的切线,
∴∠OCD=90°,
∴∠D=30°,
∴∠A=∠D,
∴AC=CD;
(2)解:∵∠OCD=90°,∠D=30°,CD=6$\sqrt{3}$cm,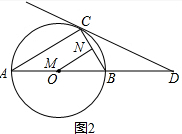
∴OC=CD•tan∠D=6,
∴AB=12;
(3)解:如图2,∠MNB=90°时,
由题意得,AM=3t,BN=1.5t,
∵AB是⊙O的直径,
∴∠ACB=90°,又∠MNB=90°,
∴MN∥AC,
∴$\frac{BM}{BA}$=$\frac{BN}{BC}$,即$\frac{12-3t}{12}$=$\frac{1.5t}{6}$,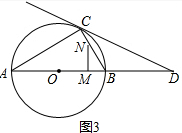
解得t=2s;
如图3,∠NMB=90°时,
△BNM∽△BAC,
∴$\frac{BM}{BC}$=$\frac{BN}{BA}$,即$\frac{12-3t}{6}$=$\frac{1.5t}{12}$,
解得t=3.2(舍去).
∴当t=2s时,△BMN为直角三角形.
点评 本题考查的是切线的性质定理、直角三角形的性质、勾股定理的应用,相似三角形的判定和性质定理,正确作出辅助线、灵活运用相关定理是解题的关键,注意分情况讨论思想的正确应用.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
17.如果一个三角形两边分别为2cm、7cm,且第三边为奇数,则此三角形为( )
| A. | 不等边三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 直角三角形 |
15.下列方程是一元二次方程的是( )
| A. | 3x2+$\frac{1}{x}$=0 | B. | 2x-3y+1=0 | C. | (x-3)(x-2)=x2 | D. | (3x-1)(3x+1)=3 |
12.为了增强居民的节约用电意识,某市拟出台居民阶梯电价政策:每户每月用电量不超过230kW•h的部分为第一档,按每千瓦时0.49元收费;超过230千kW•h且不超过400kW•h的部分为第二档,超过的部分按每千瓦时0.54元收费;超过400kW•h的部分为第三档,超过的部分按每千瓦时0.79元收费.
(1)将按阶梯电价计算得以下各家4月份应交的电费填入下表:
(2)设一户家庭某月用电量为xkW•h,写出该户此月应缴电费y(元)与用电量x(kW•h)之间的函数关系式.
(1)将按阶梯电价计算得以下各家4月份应交的电费填入下表:
| 4月份总用电量/kW•h | 电费/元 | |
| 小刚 | 200 | 98 |
| 小丽 | 320 | 161.3 |
| 小红 | 450 | 244 |
 画出△ABC的内切圆.
画出△ABC的内切圆.