题目内容
8.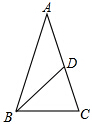 顶角为36°的等腰三角形称为黄金三角形(即:点D是AC的黄金分割点),如图,在△ABC中,AB=AC=1,∠A=36°,BD是三角形ABC的角平分线,那么AD=$\frac{\sqrt{5}-1}{2}$.
顶角为36°的等腰三角形称为黄金三角形(即:点D是AC的黄金分割点),如图,在△ABC中,AB=AC=1,∠A=36°,BD是三角形ABC的角平分线,那么AD=$\frac{\sqrt{5}-1}{2}$.
分析 先根据等腰三角形的性质和三角形内角和计算出∠ABC=∠C=72°,再根据角平分线定义得到∠ABD=∠CBD=36°,易得AD=BC=BD,然后证明△ABC∽△BCD,利用相似得性质得AC:BC=BC:CD,则AC:AD=AD:CD,于是根据黄金分割点的定义得到点D为AC的黄金分割点,易得AD=$\frac{\sqrt{5}-1}{2}$.
解答 解:∵AB=AC=1,∠A=36°,
∴∠ABC=∠C=72°,
∵BD是△ABC的角平分线,
∴∠ABD=∠CBD=36°,
∴DA=DB,
∵∠BDC=∠A+∠ABD=72°,
∴BD=BC,
∴AD=BC=BD,
∵∠A=∠CBD,∠ACB=∠BCD,
∴△ABC∽△BCD,
∴AC:BC=BC:CD,
∴AC:AD=AD:CD,
∴点D为AC的黄金分割点,
∴AD=$\frac{\sqrt{5}-1}{2}$AB=$\frac{\sqrt{5}-1}{2}$.
故答案为$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点. 其中AC=$\frac{\sqrt{5}-1}{2}$AB≈0.618AB,并且线段AB的黄金分割点有两个.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
13.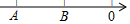 在数轴上,A、B两点的位置如图所示,那么下列说法中,错误的是( )
在数轴上,A、B两点的位置如图所示,那么下列说法中,错误的是( )
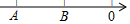 在数轴上,A、B两点的位置如图所示,那么下列说法中,错误的是( )
在数轴上,A、B两点的位置如图所示,那么下列说法中,错误的是( )| A. | 点A表示的数是负数 | B. | 点B表示的数是负数 | ||
| C. | 点A表示的数比点B表示的数大 | D. | 点B表示的数比0小 |
17.下列图形不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在Rt△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BE⊥AD交AC的延长线于F,E为垂足.则结论:(1)AD=BF;(2)CF=CD;(3)AC+CD=AB;(4)BE=CF;(5)BF=2BE,其中正确的结论个数是( )
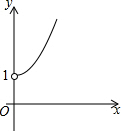
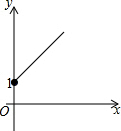
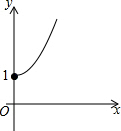
如图,在Rt△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BE⊥AD交AC的延长线于F,E为垂足.则结论:(1)AD=BF;(2)CF=CD;(3)AC+CD=AB;(4)BE=CF;(5)BF=2BE,其中正确的结论个数是( )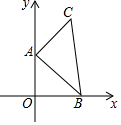 如图所示,点A的坐标为(0,1),点B是x轴上位于原点右侧的一个动点,以AB为直角边作Rt△ABC,使tan∠ABC=$\frac{3}{4}$,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
如图所示,点A的坐标为(0,1),点B是x轴上位于原点右侧的一个动点,以AB为直角边作Rt△ABC,使tan∠ABC=$\frac{3}{4}$,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )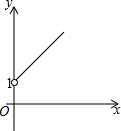
 如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1-k2=6.
如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1-k2=6.